Derivadas, un criterio para analizar funciones matemáticas
Máximos y Mínimos de una Función Cuadrática
Criterio de las DerivadasEn mi último trabajo les presenté Funciones exponenciales e igualdades matemáticas con lo que quedé intrigada fue con la forma gráfica de esas expresiones algebraicas, me refiero a las funciones:
g(X) = X2 − 2X − 15
Que van a tener la forma de una parábola, eso ya lo intuía, pero si la curvatura es hacia abajo o hacia arriba, eso es otra cosa. Para saberlo, existen algunos métodos matemáticos que nos permiten determinar esas tendencias sin necesidad de realizar las gráficas de estas funciones y uno de estos procedimientos se basa en el criterio de las derivadas, donde se analiza la función para cierto rango de valores de X y determinar si existen máximos o mínimos cuando se establece que la primera derivada de la función sea 0 (f´(X) = 0).

De esta manera se puede relacionar la pendiente de la función cuadrática en los puntos críticos que resultarían ser máximos absolutos o relativos, según se estudie en todo el rango del dominio (∀ X) o en un intervalo cerrado alrededor de un punto crítico, respectivamente. El mismo criterio se utiliza para los mínimos absolutos o relativos.
Encontrar los máximos y mínimos de g(X)
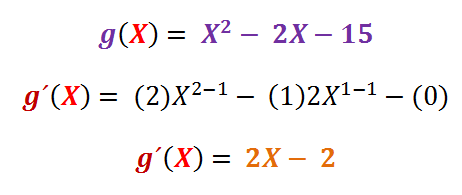
Se supone que el resultado de la primera derivada de una función está relacionada con la pendiente de la curva descrita por esta función cuadrática, siendo que forcemos a que la pendiente sea cero nos ubicaríamos en algún punto crítico correspondiente a un máximo o un mínimo, esto es, haciendo que g´(X) = 0.
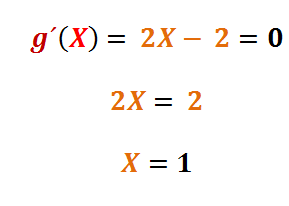
De esta manera encontramos el valor de X correspondiente a una pendiente igual a cero, es decir al punto crítico, ahora nos falta determinar el valor correspondiente a la función g(X) que sea imagen del valor X = 1
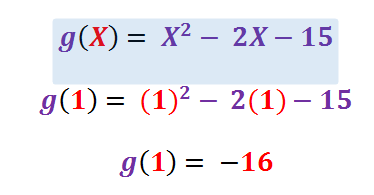
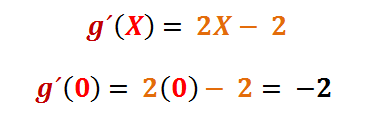
Note que estamos evaluando el comportamiento de la curva de la función cuadrática a la izquierda de Xcrítico = 1, y notamos que la pendiente = −2 es negativa o "decreciente", lo que podría ser indicativo que tiende hacia un mínimo, pero para asegurarnos de esta opción lo mejor es calcular la pendiente del lado derecho.
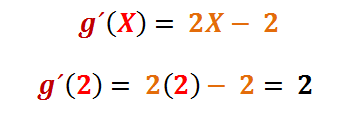
Nos tenemos que basar en el signo de la primera deriva o la pendiente calculada y vemos que en este caso es positiva, por lo que se corresponde con una tendencia "creciente", de tal manera que podemos concluir que el punto crítico (1; −16) se corresponde con un "mínimo de la función".
Sin embargo, esto no acaba aquí, ya que podemos seguir aplicando la segunda derivada de esta función y se establece que si la g´´(X) > 0 (positiva), entonces se obtendría un mínimo. Por otro lado, si la g´´(X) < 0 sería un máximo de la función. Veamos esta opción:

Note que el signo de la segunda deriva en este caso dio positiva, evaluada en el valor de Xcrítico = 1, por lo que se corresponde con un "mínimo de la función".
Permítanme salir de la curiosidad, realizaré la gráfica de la función g(X) = X2 − 2X − 15 y desarrollaremos un análisis gráfico de la función cuadrática.
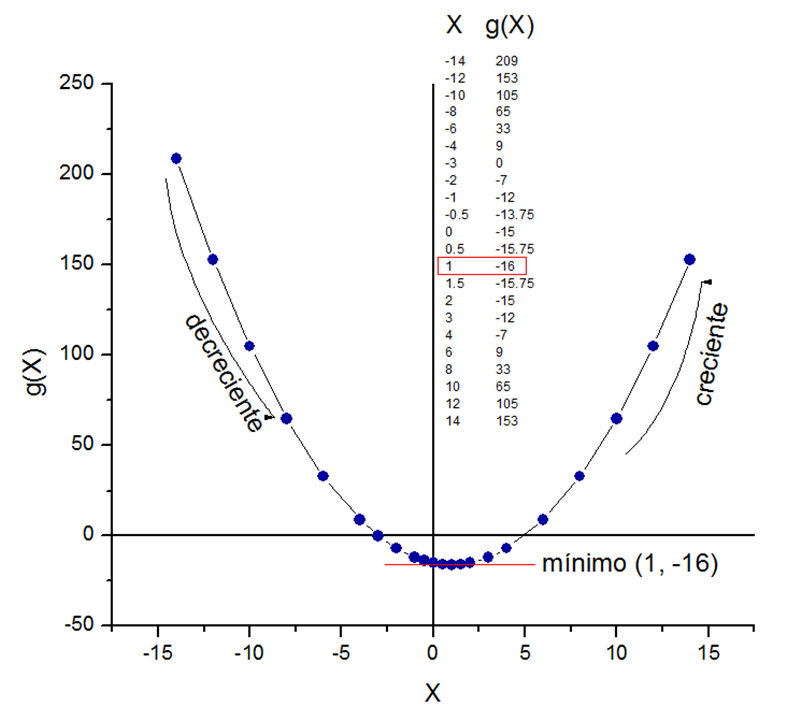
Con una sola gráfica podemos mostrar de manera visual todos los resultados de los cálculos realizados anteriormente, demostrando la certeza de que hemos aplicado los procedimientos correctos. El valor de Xcrítico = 1, en el intervalo estudiado y evaluado en la función original g(X), nos da las coordenadas del "mínimo de la función: (1; −16)", y si tratamos de expresarlo en forma matemática sería: llamando m al punto mínimo, entonces g(m) ≤ g(X) sería un mínimo para todo X (∀ X) en el intervalo cerrado (a; b), por lo que sería un mínimo absoluto.
Si se conocen los criterios de una función derivable y que la primera derivada positiva se relaciona con una tendencia creciente (g(X) > 0) y que g(X) < 0 (negativa) la función es decreciente, podemos tener las bases para inferir si estamos ante un máximo o mínimo de la función estudiada.
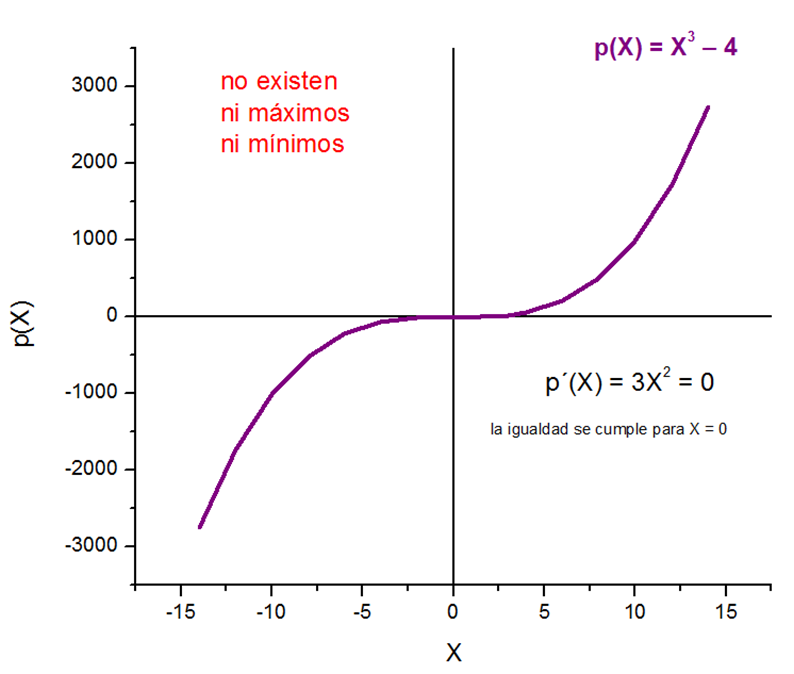
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Blog: Los máximos y los mínimos de una función
- Imagen de geralt: Estudiante y problema matemático
- Curso: Sobre los máximos y mínimos de una función
- Vídeo: Máximos y mínimos de una función
- Blog: Ejercicios de máximos y mínimos y sus soluciones
Comencemos con lo más básico,
con el planteamiento del problema!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Para practicar las derivadas recomiendo esta web que tiene bastantes ejercicios resueltos.
también en esta web de ejercicios resueltos de matemáticas