Math contest #8 Results and Solution
Solution:
The problem of the last contest was:
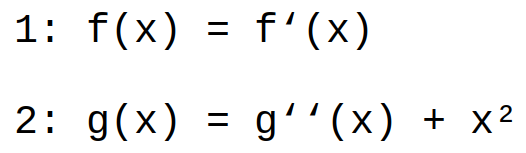
- solution:
f(x) = df(x)/dx |×dx ÷f(x)
dx = 1/f(x) × df(x) |integrate
x + C = ln(f(x)) |e^()
f(x) = e^(x+C) - solution:
Assumption:g(x) = x²+h(x)
→g''(x) = h''(x) + (x²)'' = h''(x) + 2
→h(x) = h''(x) + 2
h(x) = i(x)+2
→i(x) = i''(x)
Assumption:i(x) = e^(kx)
→e^(kx) = k²*e^(kx)
→k² = 1→k = ±1
→i(x) = A*e^x + B*e^-x
→g(x) = x² + 2 + A*e^x + B*e^-x
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
How your chance of winning is calculated:
- Every participant gets 1 point for entering the contest.
- Every solution entered gets 1 additional point.
- Multiple examples of a general solution count as one solution
- If there is only one general solution, those who found its pattern(by mentioning a general formula or showing more then 3 examples) will get an additional point.
- Your winning chance is
"your points"/"total points"
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
All participants did great and got the maximum score, but I list the score anyway.
List of participants with their scores and chance of winning, sorted by time of entry:
| Name | solutions found | score | chance of winning |
|---|---|---|---|
| @tonimontana | g(x)=c1*e^x+c2*e^(-x)+x^2+2 | 3 | 100% |
Judging by the participants it seems like differential equation is not a thing for this contest. So I'll go back to normal equation.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Congratulations @tonimontana, you won 1 SBI:

↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
The next contest starts tomorrow. Don't miss it!
0
0
0.000
Differential equations are scary for normal Steemians...
Yes I think you are right. I also do not like solving differential equations very much.