Math Contest #24 [2 SBI]
Here you can keep your brain fit by solving math related problems and also earn SBI or sometimes other rewards by doing so.
The problems usually contain a mathematical equation that in my opinion is fun to solve or has an interesting solution.
I will also only choose problems that can be solved without additional tools(at least not if you can calculate basic stuff in your head), so don't grab your calculator, you won't need it.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Rules
No upvote, No resteem, No follow required!
I will give the SBI(s) randomly to any participants.
You have 4 days to solve it.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Problem
Find the limit of the following infinite sum:
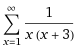
You are allowed to assume convergence because it would be easy to show.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
To everyone who already participated in a past contest, come back today and try a new problem(tell me if you don't want to be tagged):
@addax @ajayyy @athunderstruck @bwar @contrabourdon @crokkon @fullcoverbetting @golddeck @heraclio @hokkaido @iampolite @kaeserotor @masoom @mmunited @mobi72 @mytechtrail @ninahaskin @onecent @rxhector @sidekickmatt @sparkesy43 @syalla @tonimontana @vote-transfer @zuerich
In case no one gets a result(which I doubt), I will give away the prize to anyone who comments.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
@contrabourdon sponsors my contests with 2 STEEM weekly.
You can support him by using a witness vote on untersatz, so he can further support this and other contests.
Too difficult. I'm out ;-)
.
No.
This is not only because this is a math contest, but also because your result is not 100% exact.
I would say you split 1/(x*(x+3))=1/(3*x)-1/(3*(x+3))=1/3*(1/x-1/(x+3)). Now if you sum over these terms everything cancels out except 1/3*(1/1+1/2+1/3)=11/18
Hello,
Your post has been manually curated by a @stem.curate curator.
We are dedicated to supporting great content, like yours on the STEMGeeks tribe.
Please join us on discord.