Estudio de las seccione cónicas. II Parte: Hipérbola y Elipse

Saludos amigos de hive.

En esta oportunidad quiero presentarles la segunda entrega de esta corta serie temática de dos capítulos del estudio de las secciones cónicas, en este artículo se explicara la hipérbola y la elipse realizando la definición de cada uno de estos cuerpos geométricos, describiendo sus elementos más importantes y corroborando con el gráfico generado con el software geogebra5.0.

Elipse

Es importante mencionar que el origen de la elipse tuvo sus orígenes en el estudio y comprensión del movimiento de los planetas en el sistema solar. Fue el Alemán Johannes Kepler quien descubrió que los planetas se mueven alrededor del sol en forma de órbitas elípticas, teniendo al sol no como centro sino como un foco de la órbita planetaria.

Al igual como he venido desarrollando estas 4 secciones cónicas iniciare el estudio y descripción de la elipse abordando una definición tal y como lo hice con la circunferencia y la parábola, es decir definiendo a la elipse como un lugar geométrico, con la diferencia por ejemplo que para la parábola teníamos un foco, mientras que para el caso de la elipse tendremos dos focos.

Una elipse la podemos definir como el conjunto de puntos del plano (x,y) cuya suma de distancias a dos puntos fijos distintos (focos) es constante, si se unen los dos puntos focales mediante una recta, esta corta a la elipse en dos puntos llamados vértices, la recta que une a los vértices se le denomina eje mayor y su punto medio es el centro de la elipse, mientras que la recta cuya cuerda es perpendicular al eje mayor y que pasa por el centro de la elipse es el eje menor de la elipse.

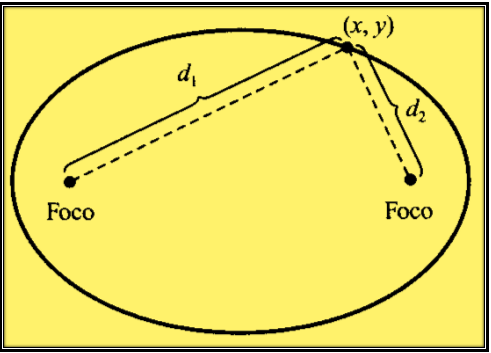
En la imagen anterior se puede apreciar los dos puntos focales, cada uno de estos puntos tienen una distancia con respecto a punto cualquiera de coordenadas (x,y) de la elipse, sin embargo podemos ver que la distancia del punto focal del extremo izquierdo al punto (x,y) (d1) tiene una distancia mucho mayor a la distancia desde el punto focal del extremo derecho al punto (x,y) (d2) y si el punto (x,y) se mueva hacia el centro de la elipse las dos distancias serán iguales, en el caso de que el punto (x,y) no esté en el centro de la elipse correspondiente a su coordenada en x siempre va existir una distancia desde el punto focal hasta el punto (x,y) mayor que la distancia desde el otro punto focal al punto (x,y).

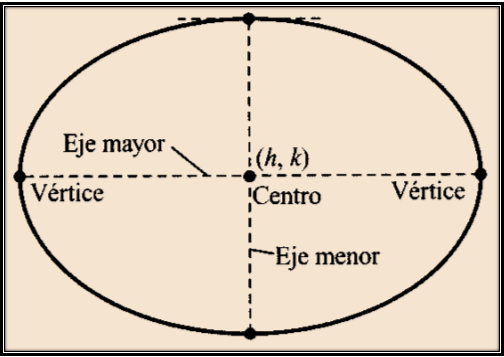
En la imagen anterior se puede apreciar que el eje mayor de la elipse es la recta que une los vértices de la elipse y que pasa por el centro de la elipse. El centro de la elipse tiene coordenadas (h,k). El eje menor es perpendicular al eje mayor y pasa por las coordenadas del centro de la elipse, por lo que podemos concluir que una elipse tiene dos puntos focales, dos ejes o rectas, uno denominado eje mayor y el otro eje menor, las coordenadas de los dos vértices, y por ultimo las coordenadas del punto que representa el centro de la elipse.

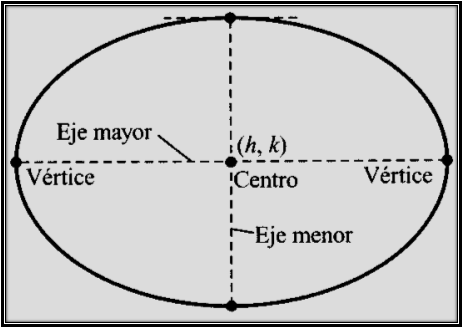
En la imagen anterior podemos apreciar todas las características de la elipse, en el que se tiene una recta horizontal que conecta los vértices de la elipse denominada eje mayor. La recta que es perpendicular al eje menor y que pasa por el centro se denomina eje menor, el punto de intercepción de los dos ejes es el centro y tiene coordenadas (h,k).

Ecuación canónica de la elipse

La ecuación canónica de la elipse considerando que el eje mayor puede ser el eje horizontal o el eje vertical, todo dependiendo de si a < b o de si a>b y teniendo las coordenadas del centro (h,k) se puede decir que la ecuación canónica es:

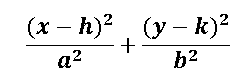
Si a>b entonces el eje mayor es horizontal.
Si b>a entonces el eje mayor es vertical.

La coordenada de los vértices se calcula de la siguiente manera:

• Si tenemos que el eje mayor está en el eje y:
  La coordenada en x=h
  La coordenada en y=k ±a

• Si tenemos que el eje mayor está en el eje x:
  La coordenada en x=h ±b
  La coordenada en y=k

Ejemplo: Dada la siguiente ecuación canónica de la elipse:

¿Encontrar el gráfico?

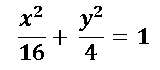
para encontrar el gráfico voy a emplear el software geogebra 5.0.

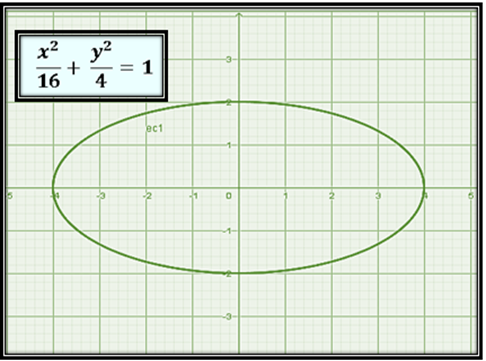
Para este caso h=0 y k=0 lo que implica que as coordenadas del centro es el origen (0,0).

La elipse corta al eje x en x1=4 y x2=-4 y al eje y lo corta en y1= 2 y y2= -2.

• a=4
• b=2

Se puede decir que los focos están en el eje mayor (eje x), a c unidades del centro, y se calcula de la siguiente manera:

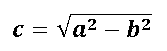
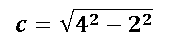
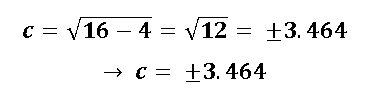
1foco = las coordenadas del punto (k+c ; h)

(h; k+c) = (0 + 3,464 ; 0) lo que implica que el 1 foco este en la siguiente coordenada (3,464 ; 0)

2 foco = las coordenadas del punto (k-c ; h)

(k-c ; h) = (0 – 3,464 ; 0) lo que implica que el 1 foco este en la siguiente coordenada (-3,464 ; 0)

La otra propiedad característica de la elipse son las coordenadas de sus dos vértices, los cuales se pueden calcular de la siguiente manera:

Como el eje mayor es horizontal, en este caso está sobre el eje x, implica que:

La coordenada en

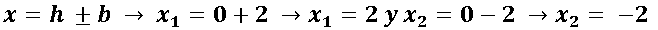
La coordenada en y=k, lo que implica que la coordenada en y = 0 para las dos coordenadas en x, lo que implica que las coordenadas de los vértices son:

V1= (2 ; 0) y V2 = (-2 ; 0)

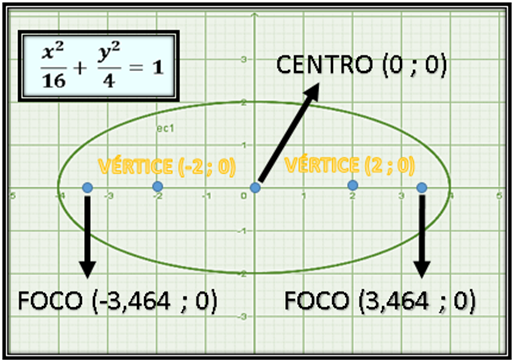
Finalmente la gráfica de la elipse con las coordenadas del foco, centro y vértices queda de la siguiente manera:

Hipérbola

Existe una similitud muy marcada entre la definición de una elipse al de una hipérbola, ya que en una elipse, la suma de las distancias de un punto de la elipse a los focos es una cantidad fija, sin embargo en una hipérbola lo que es fijo es la diferencia entre esas distancias.

Por lo antes explicado, se puede definir a la hipérbola como el cuerpo geométrico que tiene un conjunto de puntos en el plano (x,y) para los cuales las diferencias de sus distancias a dos puntos fijos distintos (focos) es constante.

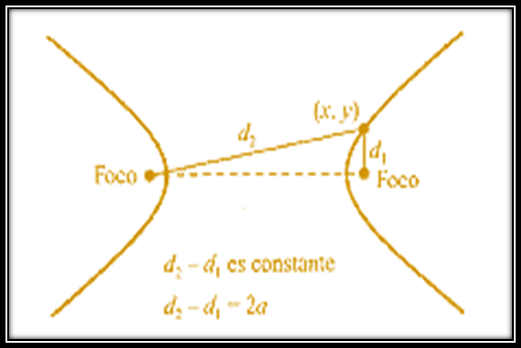
Existe una recta que pasa por los dos puntos focales y que corta a la hipérbola en dos puntos que van hacer los vértices de la hipérbola, al mismo tiempo ese segmento de recta que une los dos vértices es llamado eje transversal, el punto medio de esta recta denominada eje transversal es el punto medio de la hipérbola.

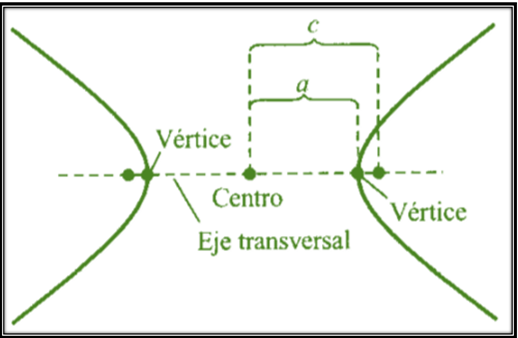
Como podemos ver en la imagen anterior, una hipérbola son como dos parábolas que abren por separado sobre un eje horizontal (eje transversal) Cada una en sus vértices, el centro de la hipérbola será el punto medio del eje transversal, a es la distancia del centro de la hipérbola a uno de sus vértices, mientras que c es la distancia desde el centro hasta uno de sus punto focales.

Ecuación canónica de la hipérbola

Cuando el eje transversal es horizontal consideramos la siguiente ecuación:

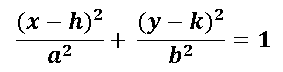
No es una regla obligada que para graficar una hipérbola se tengan que conseguir sus asíntotas, que son dos rectas que ayudad a determinar el comportamiento del gráfico, sin embargo se recomienda que se encuentre la ecuación de estas dos recta que son las asíntotas de la hipérbola. Las ecuaciones de estas dos rectas se calculan como siguen:

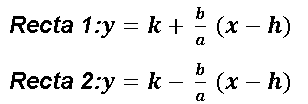
Ejemplo: Dada la ecuación de la hipérbola

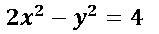
Para encontrar la ecuación canónica de la hipérbola dividimos a ambos lados de la igualdad por 4, quedando de la siguiente forma:

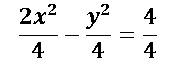
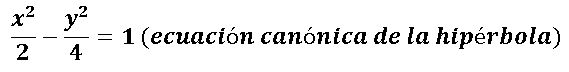
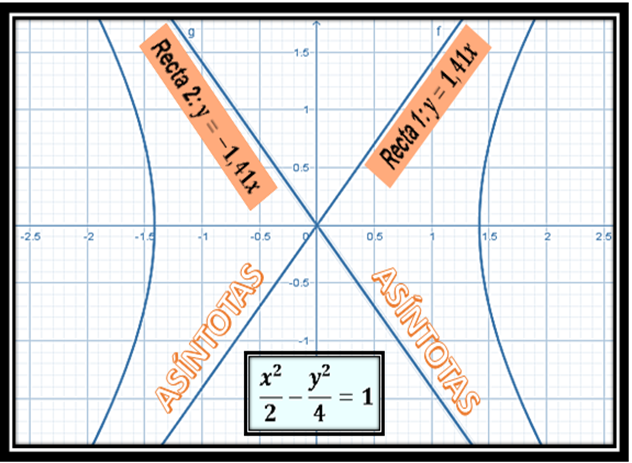
Si se hace y=0 implica que a x lo va a cortar en la raíz cuadrada de 2, que es igual a 1,41 y -1,41, al mismo tiempo estos cortes son los vértices de la hipérbola el centro de la hipérbola es el origen (0,0). Ahora voy a conseguir las ecuaciones de las a rectas que son as asíntotas de la hipérbola.

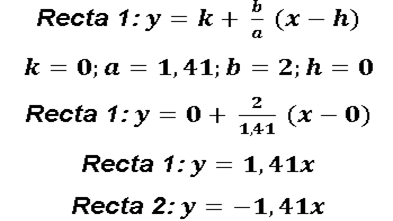
Conclusión

Es increíble saber que la elipse tuvo su origen en el estudio de los movimientos de los planetas del sistema solar, es importante mencionar que la elipse tiene dos ejes, el eje mayor y el menor los cuales pueden alternarse tanto en el eje X y el eje Y. La excentricidad de la elipse es la propiedad que mide la relación de qué tan largo es el eje mayor con respecto al eje menor.

El conocimiento adquirido sobre los elementos geométricos de la elipse puede contribuir a ciertas aplicaciones dentro de la ingeniería y las ciencias en general.

Respecto a la hipérbola desde el punto de vista geométrico debe destacarse primeramente que la hipérbola no tiene cortes con el eje Y, por lo que prácticamente la gráfica en el plano (x,y) se centra en dos parábolas que abren en el eje X.

En conclusión esta serie temática de dos capítulos que contempla el estudio de las secciones cónicas ha sido cubierto en su totalidad, abarcando así la parábola, circunferencia, elipse e hipérbola, en el que se realizó un abordaje desde el punto de vista geométrico, analítico y algebraico.

Para buscar corroborar las características geométricas de cada una de las secciones cónicas busque apoyarme empleando el software geogebra 5.0.

Nota: Todas las imágenes son propias y fueron elaboradas empleando las herramientas de diseño de imágenes de Microsoft Word y Microsoft Power Point.

Referencia consultada y recomendada

Cálculo Vol. 2 6ta Edición Roland E. Larson, Robert R. Hostetler, Bruce H. Edwards