Floating point math is the devil!
Programming exercise:
Head on over to https://playcode.io/new/
Type in:
console.log(0.1 * 125)
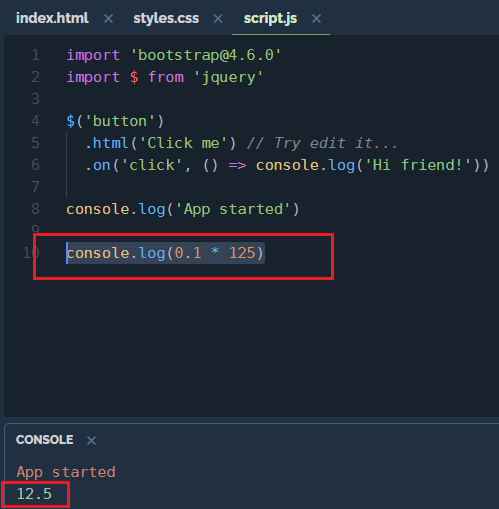
No problem!
Look at you go, you're a programmer now!
Now add a zero!
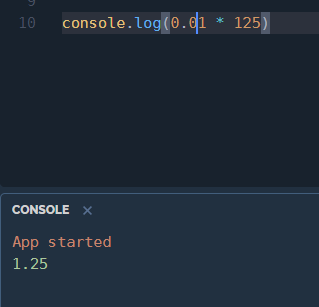
Easy, add another 0.
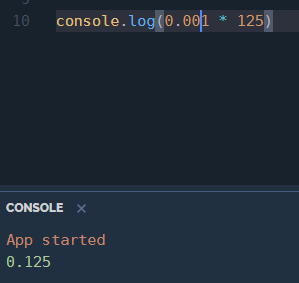
What's the point of this again?
Pipe down: add two more zeros.
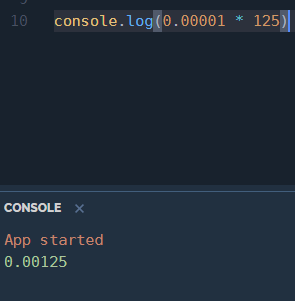
Okay, this is getting ridiculous.
Ah, so close, just two more zeros to go!
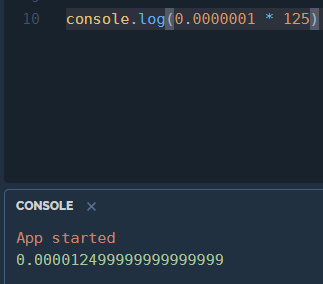
WHAT?!?!
GAH! WHY!?
How does 0.0000001 x 125 = 0.0000124999999999???
The math can't get more basic, why the rounding error?
Short answer: floating point math.

You and I are used to math being done in base 10.
- There are ten digits.
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- When multiplying or dividing by a power of 10, the decimal point moves.
Computers do math in base 2.
- There are two digits
- on/off true/false 1/0
- When multiplying or dividing by a power of 2, the decimal point moves.
So when you get into fractions, a computer can't store numbers in base two like we think of numbers in base ten. For example, try to write 1/3 in base ten. What do you get?
0.333333333333333333333...
1/3 can not be expressed perfectly as a base 10 decimal. If you were using a base 3 number system 1/3 would be 0.1 and could be expressed perfectly without a rounding error. This same thing happens with floating point math to create some weird rounding errors (often times when multiplying/dividing numbers).
https://floating-point-gui.de/formats/binary/

Who cares?
I care! DAMMIT! When you're trying to keep track of money in a database (I am) then these rounding errors become unacceptable and totally ruin database integrity. In the case of the bug I just found, I wasn't even trying to keep track of money, but rather have been working on my sliding-scale voting system.
The schedule I've developed DEPENDS on the numbers being exact. If a variable in the database gets voted up/down and becomes 0.00014999999 instead of 0.00015 my code would get very confused and stop working.
This is exactly why every database has a DECIMAL class that completely avoids floating point math and actually uses base 10. It's slower and requires more storage but the loss in performance is more than worth it to maintain database integrity in many cases (especially those involving money).
In the case of my code, I was actually using a DECIMAL when the error occurred, but I was multiplying it by another exponent that was by default a floating point number. In the background it must have cast the entire result to a float and thus there was a bug in my code.
return cast(power(10, deviation) as decimal(65,30)) * temp;
In order to fix the bug I had to CAST the exponent as a decimal in order to stop floating-point math from occurring. Problem solved.
Conclusion
Well, that's how my day is going.
Just grinding out more code.
It's been slow going but hopefully I can pick up the pace.
Market Watch Post Script:

Bitcoin shorts on Bitfinex are at local record highs.
Are the bears getting a bit too greedy?
Will there be an epic short squeeze?
Or will this market cave in once again?
Time will tell.
It gets even weirder!
I tried this in clojure...
This is the same as your result.
But then go one step further:
We are back to an accurate result!
But using the division operation instead of multiplication gives different accuracy:
Floating point arithmetic is hilarious!
Posted Using LeoFinance Beta
In computers, we have floating point math and integer math.
It is interesting that no one has done fractional math yet.
It would be a very big advantage for certain problem types.
But i also remember the days when we had an entire separate chip to do math coprocessing.
and it was mostly just a processor with registers that held floating point numbers.
And your example is why i still like C and like typed values.
To many of the modern languages will just convert types on the fly, but i really hate that, i would wish a warning about changing types.
One can do fractional math by recording the numerator and denominator separately. The problem is that the set of rational numbers is not closed over some math operations; So you have to avoid those operations. So, you really don't gain that much for all of the extra storage.
One can do fixed decimal math by remembering the location of the decimal place. I've worked on many systems that record every thing as pennies.
Of course there is a problem with every mathematical system we used because it is impossible to create a math system that is complete.
Yes, with a programmable computer, you can get it to do any kind of math... the hard way.
But think of things like Autocad. Having a 1/16 fractional system or a 1/12 fractional system would have made a lot of the math and number storage easy.
Instead you have 0.0625 and 0.41667 stored everywhere.
And, as you said, it can be imitated. And moving the decimal place to pennies, or ⅒ of pennies works well for those kinds of integers that deal with money.
I didn't understand anything I just read until I got to the last 5 lines. Good luck with that mehn.
Posted Using LeoFinance Beta
Well congratulations...my Brain officially does not compute...lol. Funny to me how I struggled to keep up with all that, and I thought I had a fair knowledge of programming ( at least python basics)
At least I can still wish you the very best of luck as the project comes along
Well floats are definitely annoying since they have those rounding errors due to the power of binary digits. All you can do is get an approximate and fix the number like you did using cast.
Well I don't plan on shorting so either way I don't mind which way it goes. So long as it goes up in the long run.
Posted Using LeoFinance Beta
Languages that do symbolic maths, such as the Wolfram language, seem to do a bit better on this front:
https://www.wolframalpha.com/input/?i=0.0000001+*+125
Posted Using LeoFinance Beta
I didn't understand much, but I found it quite interesting.
Posted Using LeoFinance Beta
made me wonder what my fav language would handle this..
tcl returned value in scientific notation to be correct, would cause formatting errors, no calc errors.
i love programming, have fun, keep light.