Discutir la continuidad de una función de dos variables apoyado con el uso de geogebra
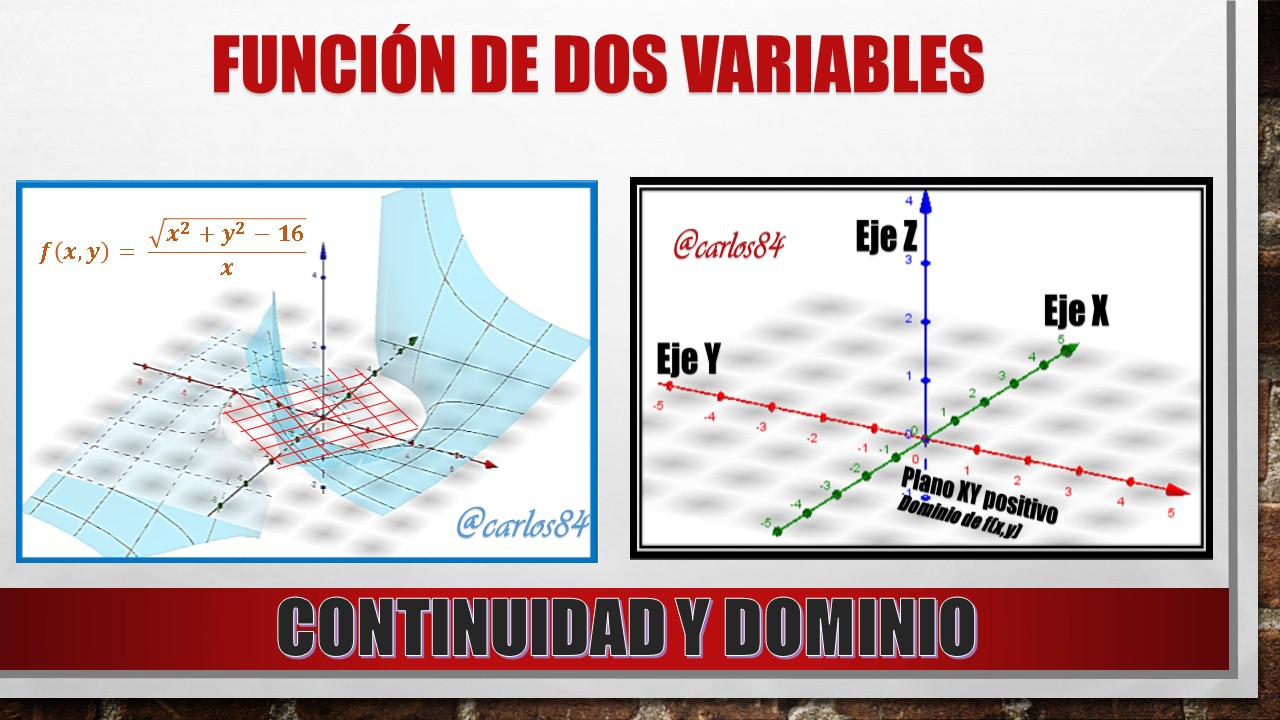
En esta ocasión quiero elegir una función de dos variables del tipo racional, la función de dos variables a elegir tiene en el numerador una parte radical, y en el denominador una parte polinómica, a continuación les presento la función de dos variables que someteremos a evaluación:
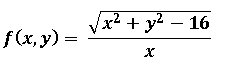
Para encontrar la continuidad de cualquier función, sea de una, dos o más variables, es necesario definir las restricciones que tenga dicha función en generar imágenes reales para todos los valores del conjunto de los números reales.
Para el caso de poder evaluar la continuidad de la función que estamos evaluando es importante determinar su dominio, para los que no saben que es el dominio de una función de dos variables, se los explico de la siguiente manera:
El dominio de una función de dos variables es el conjunto de pares ordenados (x,y) para los cuales existe una imagen real para el conjunto de partida, que en este caso es z.
Dicho de otra forma: si tenemos el plano tridimensional x,y,z el dominio de una función que se grafique en el sistema tridimensional será todos los valores del plano (x,y) para los cuales existe una relación con el eje z que es la altura. Veamos el siguiente ejemplo con la siguiente imagen:
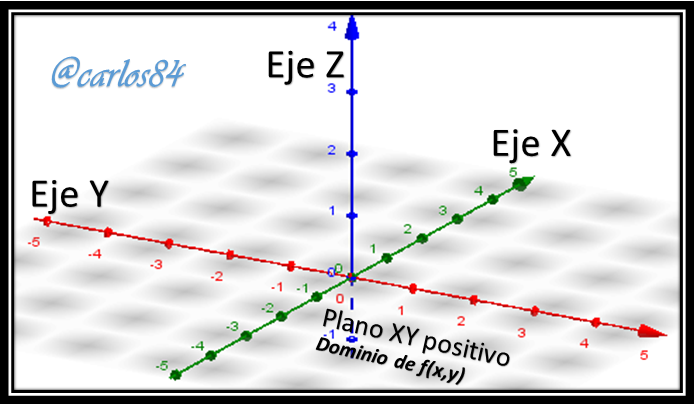
En el sistema tridimensional que pueden apreciar en la imagen anterior vamos a graficar la función de dos variables a la cual le vamos a realizar la evaluación de su continuidad, sin embargo antes de entrar en esa discusión vamos a definir los criterios de evaluación:
[1] Si el dominio existe para todos valores (x,y) que generan una imagen real en Z, entonces la función en estudio es continua en el conjunto de los números reales en el plano (x,y).
[2] Si la función tiene alguna restricción en algún conjunto de puntos del plano (x,y) entonces la función es discontinua en ese conjunto de puntos.
Después de encontrar el dominio de la función que estamos estudiando en este caso, vamos a corroborar el gráfico del dominio de la función en el plano (x,y) para determinar exactamente cuáles son los puntos del dominio que hacen a la función continua, y cuales puntos del plano (x,y) no pertenecen al dominio que hacen que la función sea discontinua en esos puntos.
Procedemos entonces a encontrar el dominio de la función de forma algebraica:
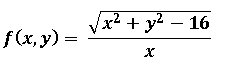
Antes de empezar es importante darnos cuenta que existen dos restricciones en esta función racional, que son:
[1] Todo lo que está dentro de una raíz cuadrada debe ser positivo para que se genere una imagen real. Por lo tanto se debe cumplir con la siguiente condición:
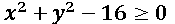
La condición anterior genera una inecuación lineal, en la cual si despejamos el 16 nos da la ecuación de una circunferencia:
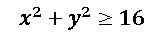
Al resolver la inecuación nos damos cuenta que el dominio de la función son todos los puntos que están fuera de la circunferencia. Por lo que es importante que grafiquemos la circunferencia y veamos los puntos que pertenecen al dominio:

Todos los puntos pertenecientes al plano (x,y) que están de color blanco pertenecen al dominio de la función.
Mientras que todos los puntos que esta sobre la línea que delimita el radio de la función y los puntos que están dentro de la circunferencia no pertenecen al dominio de la función.
[2] Como la división entre cero no está definida, entonces la segunda condición es que cuando x=0 la función es discontinua, y x=0 no pertenece al dominio de la función.
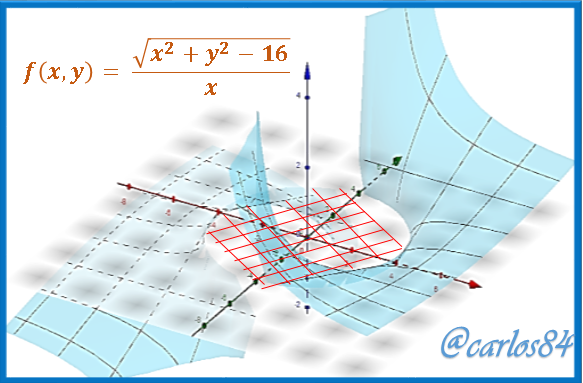
Gráfico de la función 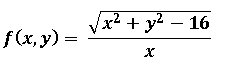 en el sistema tridimensional
en el sistema tridimensional
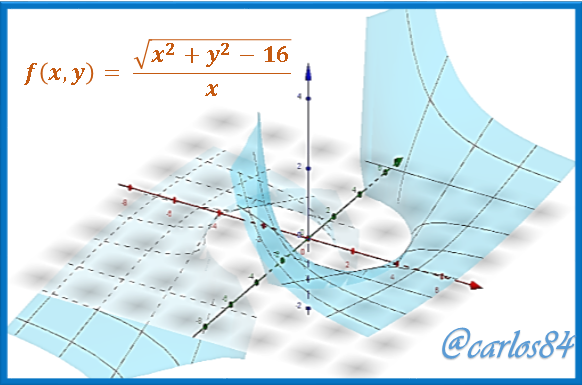
Si observamos con detenimiento el gráfico anterior podemos analizar que los dos planos de alguna manera u otra generan un zona vacía que se proyecta en el plano (x,y) que es la circunferencia de radio 4 que graficamos en el plano (x,y) que no pertenece al dominio de la función, y que hace que la función sea discontinua en esos puntos:
Espero que este post proporcione a los estudiantes universitarios en época de aislamiento social una oportunidad para ampliar sus conocimientos sobre y cálculo, hasta una próxima entrega se despide su amigo @carlos84.
Observaciones
- Todas la imágenes son de mi autoría y fueron elaboradas empleando las herramientas de diseño de Microsoft Power Point, también emplee el uso del software geogebra 5.0 para la realización de los gráficos mostrados en este post.
Referencia consultada y recomendada
Cálculo Vol. 2 6ta Edición Roland E. Larson, Robert R. Hostetler, Bruce H. Edwards. Descarga en PDF
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo. Saludo
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo. Saludo