Cálculo del área de intersección entre una función cúbica y una lineal
Saludos amigos hivesianos.
En esta ocasión quiero explicar la forma en la que podemos calcular el área de intersección entre dos funciones que generen dos secciones de área simétricas.
Para este caso las dos funciones que deseamos interceptar para calcular su área de intersección son:
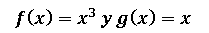
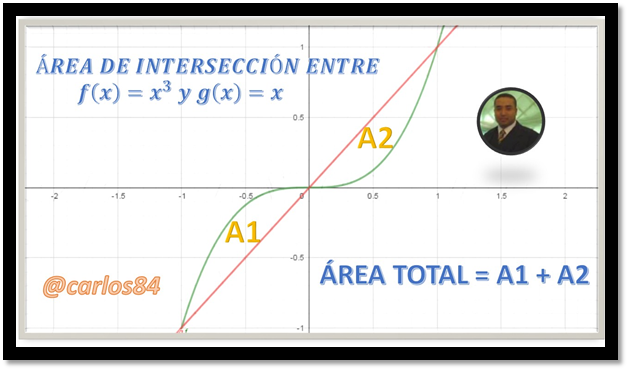
Una de las particularidades de este caso es que la función lineal intercepta a la función en x= -1; x=0 y x=1 dividendo el área total de intersección en dos sub áreas, como las dos sub áreas son simétricas (equivalentes), podemos decir que el área total es: A= A1+A2.
Otra forma de calcular el área total es calcular una sola área, por ejemplo para este caso calcular el área (A2) y la multiplicamos por 2, todo esto por la razón de que las dos secciones de áreas son simétricas.
Para comprender lo que se desea conseguir, a continuación muestro la siguiente imagen propia que elabore empleando el software geogebra 5.0 y editándola en Microsoft Power Point:

Como ya lo ha explicado en post anteriores, para calcular el área de intersección entre dos funciones lo hacemos aplicando una de las aplicaciones que tiene el cálculo integral:
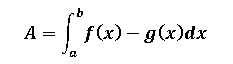
Resulta necesario explicar que f(x) es la función que está por encima de la sección del área de intersección que vayamos a calcular, en el caso del presente post vamos a calcular A2 y el valor que nos dé lo vamos a multiplicar por dos ya que las dos secciones de área son simétricas, para A2 la función que está por encima es la función lineal [f(x)= x] y la función que está por debajo es la función cúbica.
Sin embargo es importante resaltar que en el caso que se desee calcular el área total calculando A1 por dos se debe considerar que la función que está por encima es la función cúbica y la función que está por debajo es la función lineal, si realizamos la sustitución nos queda:
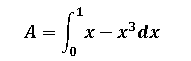
Para resolver la integral planteada es necesario resolver la integral indefinida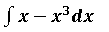
Como existen dos términos que los separa el signo negativo implica que debemos de integrar cada uno de esos términos, para cada uno de esos términos se aplica la siguiente regla básica de integración: 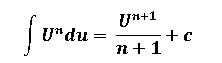
Para resolver
∫xdx
implica que U=x y n=1, por lo tanto:
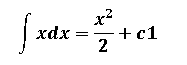
Para resolver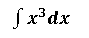 implica que U=x y n=3, por lo tanto:
implica que U=x y n=3, por lo tanto:
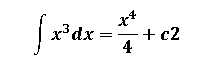
La integral indefinida:
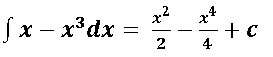
Para resolver la integral definida:
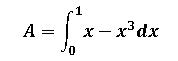
Simplemente aplicamos el teorema fundamental del cálculo, el cual expresa lo siguiente:
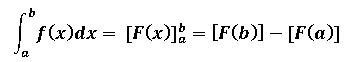
Si tomamos en cuenta que [F(x)] es la antiderivada implica que:
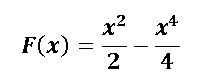
Los límites de integración son a=0 y b=1 lo que implica que:
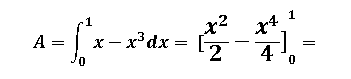
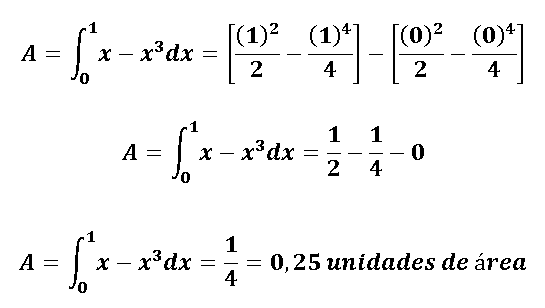
El área total A= 2 x 0,25 = 0,50 unidades de área.
Conclusión
Existen funciones que se pueden interceptar en varias secciones, tal es el caso de la función cúbica y función lineal presentadas en el ejemplo de este post, lo importante del caso es que si las secciones son simétricas, solo es necesario calcular una de las secciones y multiplicar por la cantidad de secciones que salgan en la intercepción.
Para el caso del ejemplo solo tomamos una sola sección de área (A2) y multiplicamos por dos.
Las secciones son simétricas ya que el área A1 va desde x=-1 hasta x=0 y A2 va desde x= hasta x=1
Nota: Todas las imágenes y ecuaciones son de mi autoria y fueron elaboradas empleando las herramientas de diseño de Microsoft Word y Microsoft Power Point.
Referencia recomendada para ampliar el aprendizaje
https://twitter.com/CARLOSJB84/status/1318618441566343179
posh:
https://twitter.com/CARLOSJB84/status/1318618441566343179
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDAD, apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Saludos amigos entropicos, gracias por el apoyo.
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo a @cervantes y @ramonycajal. Saludos