Artificial Neurons: Sigmoids
This is the second post in a series on neural networks and deep learning. This series is my attempt to get more familiar with the topic and is heavily based on the book by Michael Nielsen.
In this post we will be looking at something called a sigmoid. A sigmoids are artificial neurons similar to perceptrons discussed in the previous post. However, as will become apparent in this post, they are extremely useful for neural networks and machine learning.
Suppose we have constructed a neural network using perceptrons. If we train this network to do a certain task, we want to make sure that a small change in a bias or weight, only has a small influence on the behavior of the network. From what we have seen in the previous post, this is not the case with a network of perceptrons. A slight change of a bias or weight can change a perceptron's output from 0 to 1 (or vice versa). In turn, such a change can completely alter the behavior of the neural network.
When training a neural network, it is not desirable to have neurons the respond in a binary fashion to their input. In other words, what we want is that for a small change in weight or bias, the output signal is only slightly changed. Perceptrons, with their basic binary (on/off-type) output, are simply not usable for this.
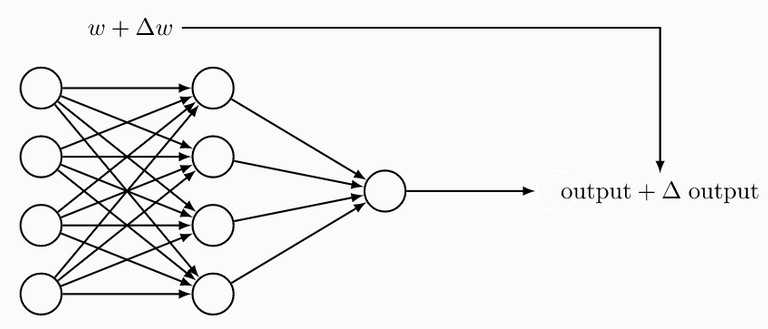
Sigmoid neurons, are the solution to the binary ouptut of perceptrons. Sigmoids have a small ouput variation when slightly changing it's weight or bias. This allows us to train a sigmoid-based neural network. A sigmoid, similarly to a perceptron, takes one or more input variables, and uses these to provides an output signal.
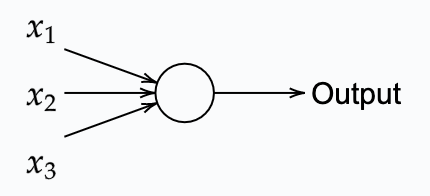
The key difference, however, is that sigmoids accept any signal between 0 and 1, and similarly, its output can be anywhere between 0 and 1. E.g. 0.638 could be a valid input for a sigmoid neuron. Sigmoid neurons also comes with weights for each input $w_1$, $w_2$ and $w_3$ for the example given in the figure above. Similarly, it comes with an overall bias $b$. The non-binary output, on the other
hand, is defined as $\sigma (w\cdot x + b)$, where $\sigma$ is the so-called sigmoid function defined by:
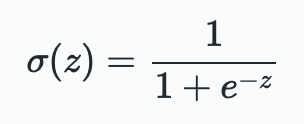
$\sigma$ is also called the logistic function, and this new class of neurons called logistic neurons. These terms are used by many people working with neural nets. It's useful to remember this.
Using the input, weights, and bias, the sigmoid output can be written as:

Although his looks quite different from perceptrons, the basic idea is quite similar. Suppose $z\equiv w \cdot x +b$ is a very large number, then $\sigma(z)\approx 1$. In other words for large weights and bias, the sigmoid has an output close to one. This is very similar to perceptrons. On the other hands when the weights and bias are very large negative numbers, $z \to \infty$, and thus $\sigma(z)\approx 0$. Only when $z$ is in the mid-range, the sigmoid differs significantly from perceptrons.
Perhaps when looking at the shape of a sigmoid function its affect becomes more clear:
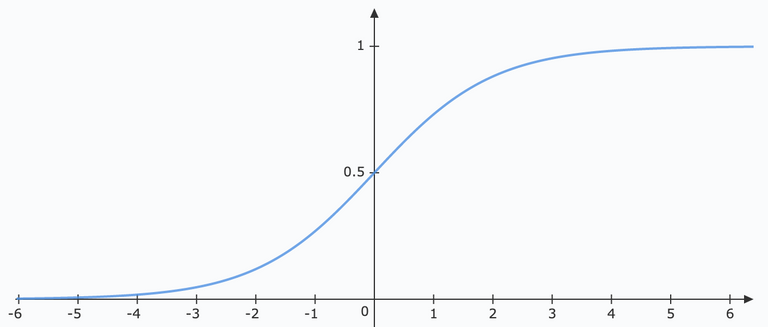
This function is not just one or zero like that of a perceptron. In fact its a smoothed version of a perceptron function shown below:
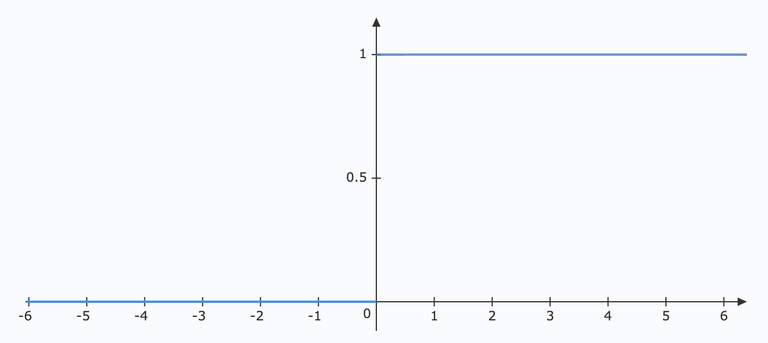
If the sigmoid function would have been defined as a step-function, it would in fact be a perceptron! This, because the output would be either 0 or 1 depending on $\sigma$ being negative or positive.
The smoothness of $\sigma$ makes it, that small changes $\Delta w_j$ or $\Delta b$ result in mall changes $\Delta \text{output}$. Using a bit of calculus, one could even write:
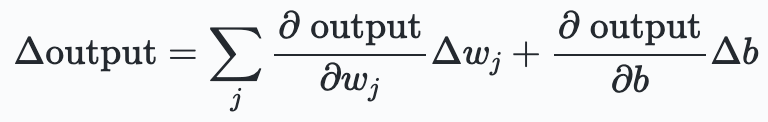
This expression says that $\Delta \text{output}$ is linearly depending on the $\Delta w_j$ and $\Delta b$. Despite the fact that sigmoids show very similar qualitative behaviour as perceptrons, this linearity allows us to figure out how changing weights and biases changes the output. And in a system of neurons, this allows for learning.
In principle, one could use other types of functions in place of $\sigma$. In fact, in the field of NN and ML, different functions are used for different occasions. However, in most common theory the $\sigma$ functions are used due to their simplistic derivative properties.
Hope you enjoyed tagging along my journey into the world of Neural networks. In the next post we will be looking more into the general architecture of a neural network. These networks consist of multiple sigmoid or perceptrons combined together.
Testing comment