Fundamental Theorem of Calculus - Introduction and Part 1 of the Theorem
In this video I introduce one of the most important mathematical discoveries and in fact one of the most important discoveries in general that mankind has discovered, and that is the Fundamental Theorem of Calculus! I introduce the theorem by giving a brief history lesson on it and later illustrate how integral and differential calculus are linked with this Fundamental Theorem by showing that the two branches of calculus are inversely related; i.e. the derivative of the integral is the function it is integrating!
Watch video on:
- 3Speak:
- BitChute: https://www.bitchute.com/video/4e23CbwqA8zz/
- DTube: https://d.tube/#!/v/mes/QmbhMES8kimzZZ3F6NyMmJtWcPcdq7cGCafQcxjRjm1U3z
- YouTube: https://youtu.be/3o8Q6UJzJyk
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiZMw-_HRsud1rXujiQ?e=kJmW3V
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Subscribe to MES Truth: https://mes.fm/truth
MES Links Telegram channel: https://t.me/meslinksJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Fundamental Theorem of Calculus - Introduction and Part 1 of the Theorem
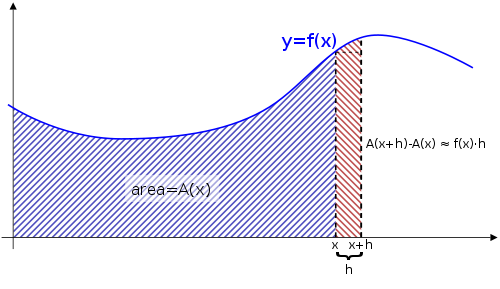
Introduction
- The Fundamental Theorem of Calculus is appropriately named because it forms a connection between the 2 branches of calculus: Differential and Integral Calculus.
- Differential calculus arose from the tangent problem.
- Integral calculus arose from the area problem.
- Newton’s teacher at Cambridge University (UK), Isaac Barrow (1630-1677), discovered that integral and differential calculus are closely related, in fact he realized they were inverse processes.
- The Fundamental Theorem of Calculus gives the precise inverse relationship between the derivative and the integral.
- Newton and Leibniz exploited this relationship and used it to develop calculus into a systematic mathematical method.
- In particular, they saw that the Fundamental Theorem enabled them to compute areas and integrals very easily without having to compute them as limits of sums as in my earlier videos.
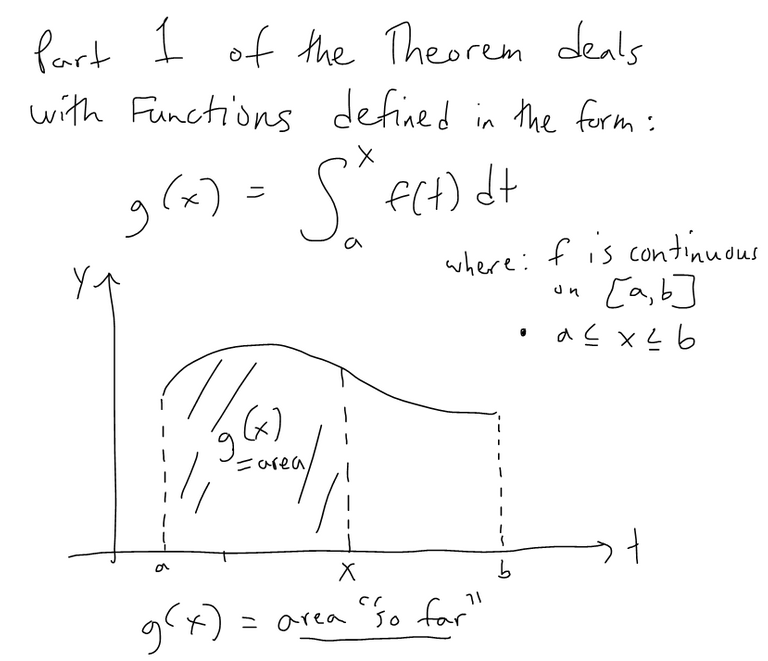
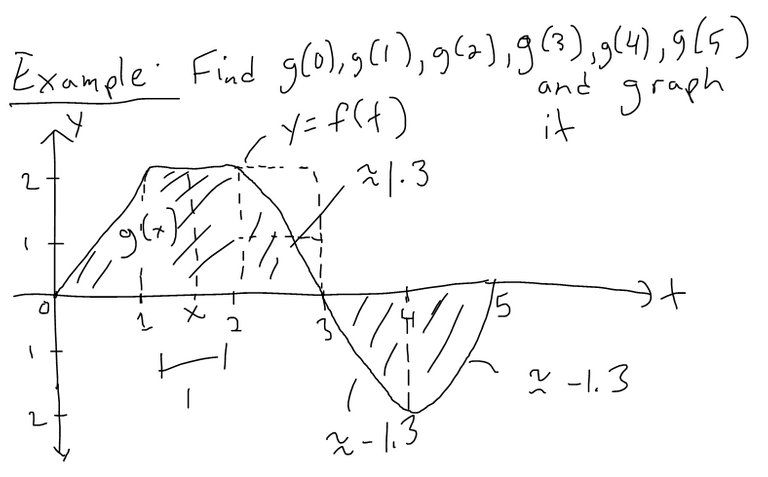
Part 1 of the Theorem
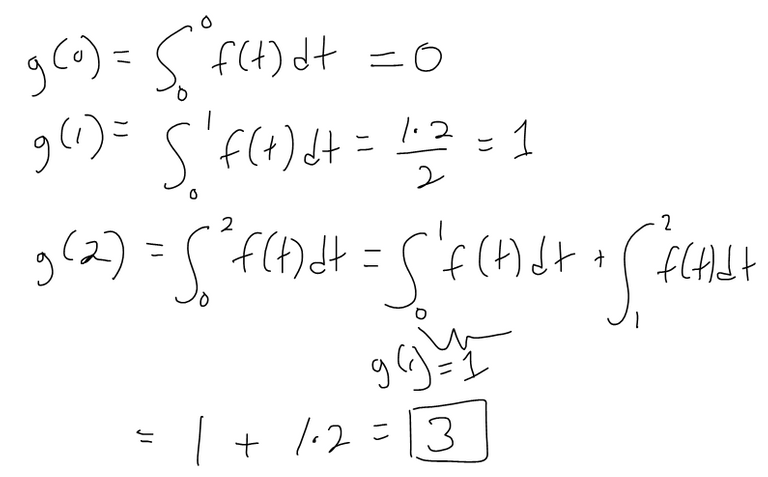
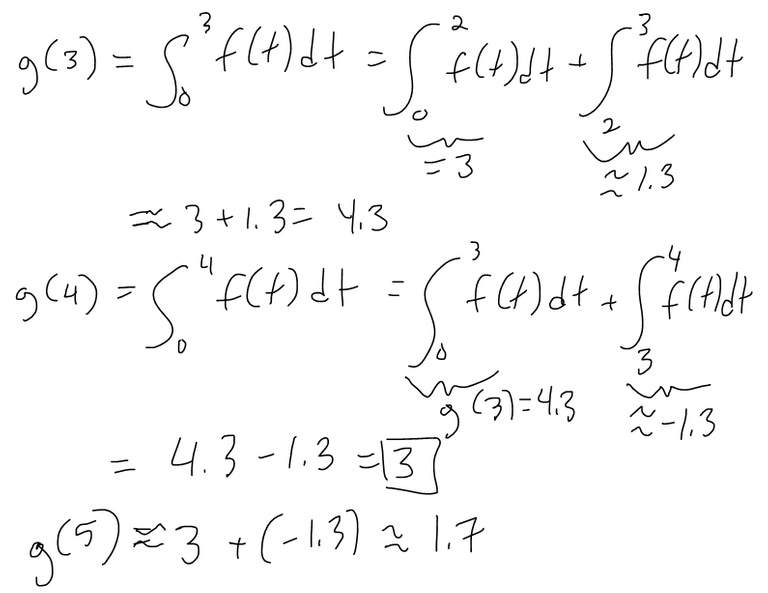
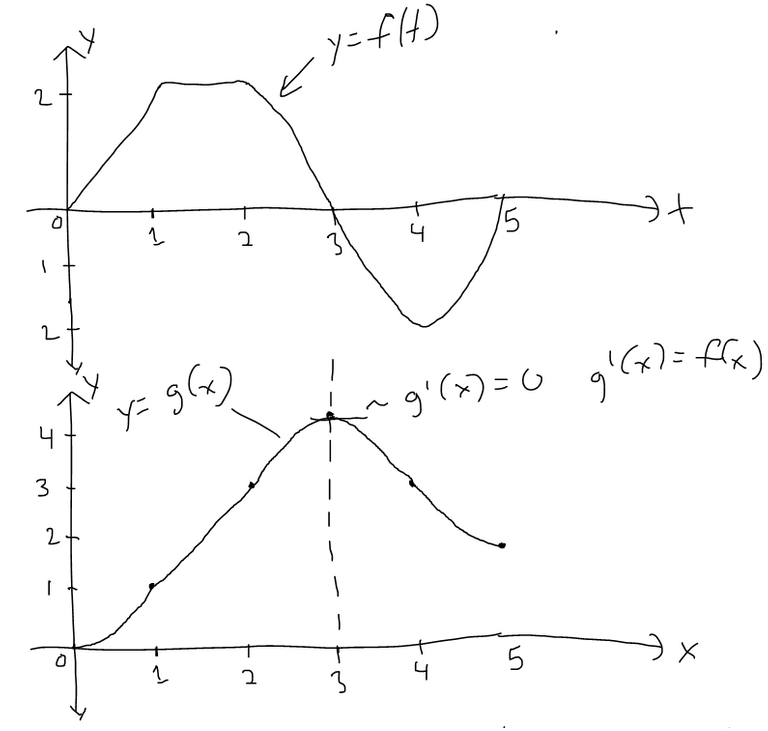


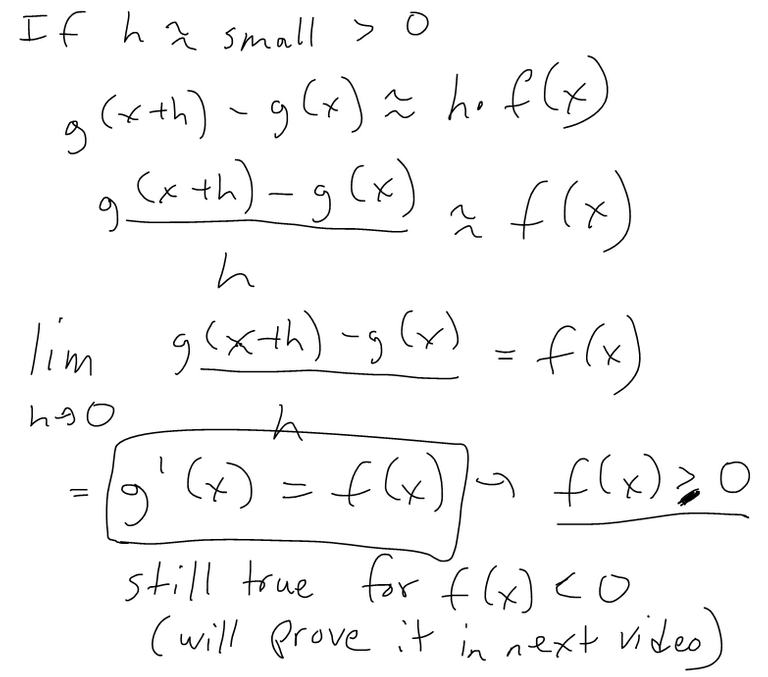

https://twitter.com/MathEasySolns/status/1549822138533572609
The rewards earned on this comment will go directly to the people( @mes ) sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.