Applied Project: Radiation from the Stars (Blackbody Radiation)

avatar
(Edited)

In this video I go over another Applied Project and titled “Radiation from the Stars”. This is an interesting project from my calculus book at the end of the section on Infinite Sequences and Series. The project involves blackbody radiation and comparing the classical model with the newer quantum mechanics model.

Blackbody radiation is the heat radiation of a simplified ideal object that absorbs all incoming radiation and emits radiation that is dependent only on temperature of the object and not the frequency of the incoming radiation. Objects such as a furnace blast, matte black, and superheated objects like the Sun behave as blackbody radiators.

In the 19th century, John William Strutt aka “Lord Rayleigh” and James Jeans had derived a theoretical model for the radiation spectrum of a blackbody, but this diverged significantly from known experimental findings, in particular at low wavelengths or high frequency light. This resulted in what is known as the Ultraviolet Catastrophe.

In 1900, Max Planck looked to resolve this by postulating that light can only exist in discrete packets or quanta and not at any arbitrary value. This quantization of light produced experimentally accurate results for blackbody radiation and ushered in the start of “Quantum Mechanics”.

In this particular Applied Project, I go over Planck’s Law, determine its limits, and show that at high wavelengths the law converges to Rayleigh-Jeans Law.

Later in the video I make a note regarding Planck’s Constant and a potentially better interpretation of the quantization of energy from the YouTuber Lori Gardi aka Fractal Woman. I had initially written up a more extensive derivation of Planck’s Law in this video, but I have since removed it to do as a separate video in the future. Nonetheless, I have included the following links for further research:

  • Derivation of Planck’s Law by “Physics Explained”:
  • Interpretation of Plank’s Constant by “Fractal Woman”: https://peakd.com/hive-128780/@mes/cycles-planck-s-constant-and-the-true-nature-of-light

    • The topics covered in this video are listed below with their time stamps.

    • @ 0:00 – Intro
    • @ 1:34 - MES Note: Sharpen Your Mind with Mathematics
    • @ 3:31 - Calculus Book Reference
    • @ 3:45 - Topics to Cover
    1. @ 4:16 - Note on Applied Projects
    2. @ 4:37 - Applied Project: Radiation from the Stars
      • @ - 13:23 - 5 Questions
    3. Solutions
      • @ 15:44 - Solution to Question 1
      • @ 40:33 - Solution to Question 2
      • @ 51:00 - Solution to Question 3
      • @ 56:04 - Solution to Question 4
      • @ 56:44 - Solution to Question 5
    4. @ 1:02:08 - Quick Review of Planck's Law
      • @ 1:11:28 - MES Note on Planck's Constant

    Watch Video On:

    Download Video Notes:

    View Video Notes Below!

    Download these notes: Link is in video description.
    View these notes as an article: https://peakd.com/@mes
    Subscribe via email: http://mes.fm/subscribe
    Donate! :) https://mes.fm/donate
    Buy MES merchandise! https://mes.fm/store
    More links: https://linktr.ee/matheasy

    Reuse of my videos:

    • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

    Fight back against censorship:

    • Bookmark sites/channels/accounts and check periodically
    • Remember to always archive website pages in case they get deleted/changed.

    Recommended Books:
    "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
    Subscribe to MES Truth: https://mes.fm/truth

    Join my forums!

    Follow along my epic video series:

    NOTE #1: If you don't have time to watch this whole video:

    Browser extension recommendations:

    Applied Project Radiation from the Stars.jpeg

    MES Note: Sharpen Your Mind with Mathematics

    In my last video, I gave an update about my progress for MES Science 3, which will now be on Microbiology and Genetics.

    I have spent 5+ months researching all things COVID-19 and biology in general but at the expense of making my usual math videos; thus I am taking a quick break to get in a math video!

    I have always viewed mathematics as one of, if not the best, tools to help sharpen the mind and was the driving force in deciding to create Math Easy Solutions.

    Mathematics has several key aspects that make it applicable to all areas of life:

    1. Assumptions and principles are clearly defined.
    2. Logical progression of steps when making derivations.
    3. Results in exact or quantifiable answers.
    4. Different answers can be modeled by changing assumptions/principles.
      • This is a usual technique of corporate / government deception.
    5. Can individually validate the derivation of others.
    6. Validated derivations can be used in other derivations.
    7. Can brute-force validate derivations with a computer.

    These aspects could be categorized as the term "logic", which is severely lacking in the world right now.

    With this in mind, let's dive in!

    Calculus Book Reference

    Note that I mainly follow along the following calculus book:

    Calculus: Early Transcendentals Sixth Edition by James Stewart

    Topics to Cover

    1. Note on Applied Projects
    2. Applied Project: Radiation from the Stars
      • 5 Questions
    3. Solutions
      • Solution to Question 1
      • Solution to Question 2
      • Solution to Question 3
      • Solution to Question 4
      • Solution to Question 5
    4. Quick Review of Planck's Law
      • MES Note on Planck's Constant

    Note on Applied Projects

    Recall that Applied Projects are interesting math projects at the end of some sections of my calculus book.

    In this particular project, they are at the end of the chapter on Infinite Sequences and Series.

    Applied Project: Radiation from the Stars

    Any object emits radiation when heated.

    A blackbody is a system that absorbs all the radiation that falls on it.

    For instance, a matte black surface or a large cavity with a small hole in its wall (like a blast furnace) is a blackbody and emits blackbody radiation.

    MES Note: Essentially a blackbody absorbs all incoming light and emits outgoing light that is not dependent on the type of incoming light.

    The outgoing light is dependent only on its temperature and a good approximation is a small hole inside a hollow object.

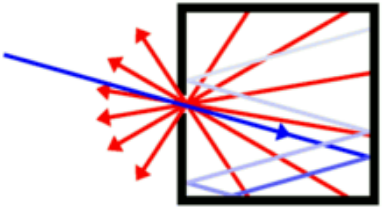
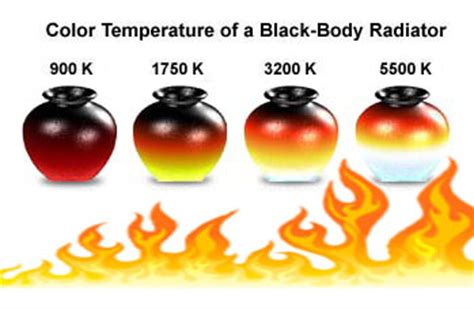
    image.png

    image.png

    image.png

    Note that blackbody radiation doesn't depend on the shape of the object, just the temperature.

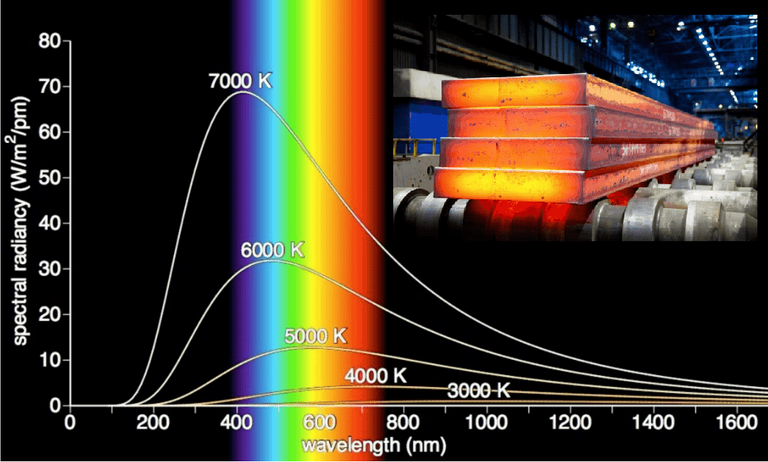
    image.png

    image.png

    image.png

    Note that the temperature of the Sun is 5700 K which has a spectral peak mainly in the visible light range.

    Even the radiation from the sun is close to being blackbody radiation; that is the radiation emitted is almost entirely a result of heat.

    image.png

    MES Note: Frequency and wavelength are related to each other:

    Wavelength = periodic distance between waves or cycles.

    Frequency = waves or cycles per second.

    For light or radiation, the shorter the wavelength the higher the frequency (and energy) as per the following expression: f = c/λ.

    Proposed in the late 19th century, Rayleigh-Jeans Law expresses the energy density of blackbody radiation of wavelength λ as:

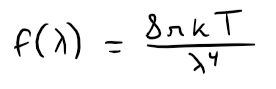
    image.png

    Where:

    • λ is measured in meters
    • T is the temperature in kelvins (K)
    • k is Boltzmann's constant.

    MES Note: Boltzmann's constant is a proportionality factor that relates kinetic energy of particles in a gas with the thermodynamic temperature of the gas; that is, temperature is defined based on the average kinetic energy of a collection of non-interactively moving particles. Boltzmann's constant is also applied to electromagnetic waves.

    The kelvin (K) is the base unit of temperature in the International System of Units (SI); water freezes at 273.15 K (0°C or 32°F) and boils at 373.15 K (100°C or 212°F).

    (Water boiling - Water Freezing) = 100 K or 100°C or 180°F

    0 K or absolute zero is assumed as the lowest motion of ideal gases, which are based on a simplified model of point particles (having no spacial dimension) and don't have interparticle interactions such as attraction or repulsion.

    The Rayleigh-Jeans Law agrees with experimental measurements for long wavelengths but disagrees drastically for short wavelengths.

    The law predicts that f(λ) → ∞ as λ → 0+ but experiments have shown that f(λ) → 0.

    This fact is known as the ultraviolet catastrophe.

    In **1900 **Max Planck found a better model (known now as Planck's Law) for blackbody radiation:

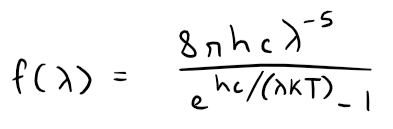
    image.png

    Where:

    • λ is measured in meters (m)
    • T is the temperature in kelvins (K)
    • h is Planck's constant = 6.6262 x 10-34 J∙s
    • k is Boltzmann's constant = 1.3807 x 10-23 J/K
    • c is speed of light = 2.997925 x 108 m/s

    MES Note: Planck's constant is the "quantum of action" and is multiplied by a photon's frequency to obtain its energy.

    Question 1

    Use l'Hospital's Rule to show that Planck's Law results in the following:

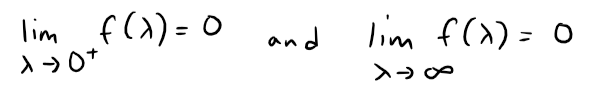
    image.png

    So this law models blackbody radiation better than the Rayleigh-Jeans Law for short wavelengths.

    Question 2

    Use Taylor polynomials to show that, for large wavelengths, Planck's Law gives approximately the same values as the Rayleigh-Jeans Law.

    Question 3

    Graph f as given by both laws on the same screen and comment on the similarities and differences.

    Use T = 5700 K (the temperature of the sun).

    You may want to change from meters to the more convenient unit of micrometers: 1 µm = 10-6 m.

    Question 4

    Use your graph in Problem 3 to estimate the value of λ for which f(λ) is a maximum under Planck's Law.

    Question 5

    Investigate how the graph of f changes as T varies (using Planck's Law).

    In particular, graph f for the stars Betelgeuse (T = 3400 K), Procyon (T = 6400 K), and Sirius (T = 9200 K) as well as the sun.

    How does the total radiation emitted (the area under the curve) vary with T?

    Use the graph to comment on why Sirius is known as the blue star and Betelgeuse as the red star.

    Solutions

    Solutions to Question 1

    Recall l'Hospital's rule from my earlier video:

    https://youtu.be/FhFWfVUBXC4
    Retrieved: 3 October 2020
    Video notes archive: https://archive.vn/qiZ5r

    image.png

    Let's take a look at the following limits, while grouping the constants together to simplify the equation.

    image.png

    In both cases, we can use l'Hospital's Rule.

    Let's do the limit at infinity first.

    image.png

    The limit at zero (from the right or positive side) requires several iterations of the l'Hospital's Rule.

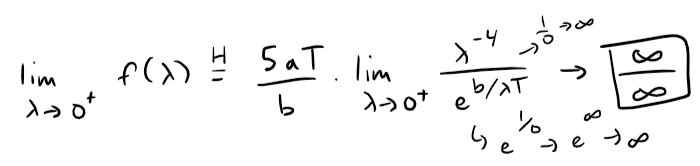
    image.png

    This is still indeterminate, but note that each time we use l'Hospital's Rule, we gain a factor of λ in the numerator, as well as a constant factor, and the denominator is unchanged.

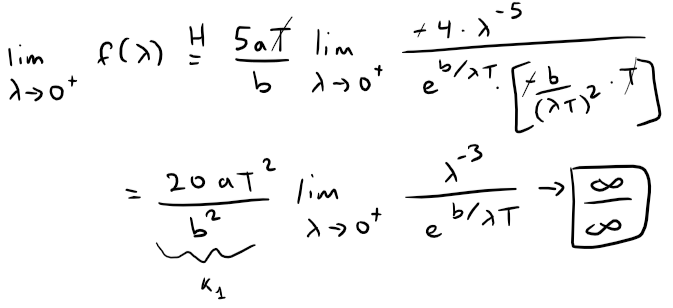
    image.png

    If we use the l'Hospital's Rule three more times, the exponent of λ in the numerator will become 0.

    That is, for some constant {ki}, all constant, then:

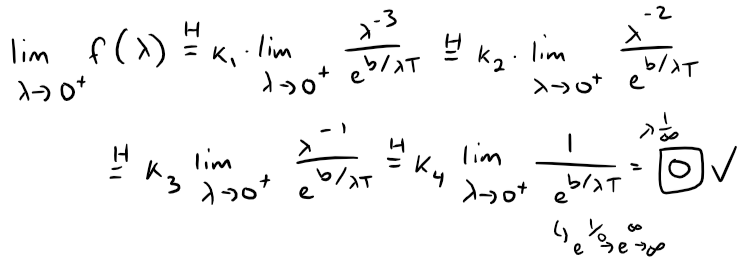
    image.png

    This confirms question 1.

    Solution to Question 2

    We can approximate Planck's Law by expanding the exponential function using a Taylor polynomial.

    First a quick recap on Taylor series from my earlier video.

    https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
    Retrieved: 24 September 2020
    Archive: https://archive.is/w3n31

    image.png

    image.png

    image.png

    image.png

    From the table above, we can use the following Taylor series:

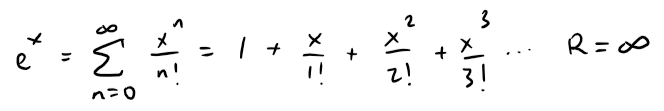
    image.png

    Thus we have:

    image.png

    This is exactly Rayleigh-Jeans Law!

    Thus, since λ is large and the terms of the Taylor series are very small compared with the first (non-zero) term, approximating Planck's Law using just the first Taylor polynomial, T1, yields Rayleigh-Jeans Law.

    Solution to Question 3

    To convert to µm, we multiply λ(m) * 106 (µm/m) = λ(µm).

    https://1drv.ms/x/s!As32ynv0LoaIiOJYlASx_wQiNRglYw?e=P9zfdM
    Retrieved: 16 May 2021
    Archive: Not available

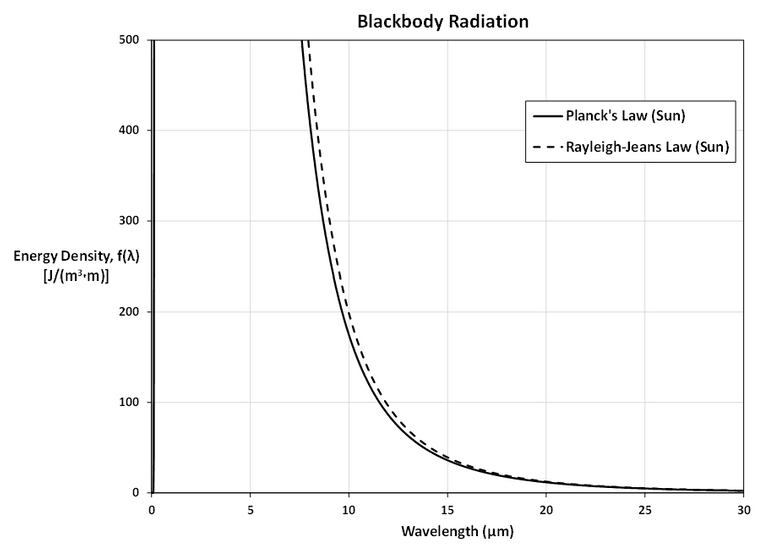
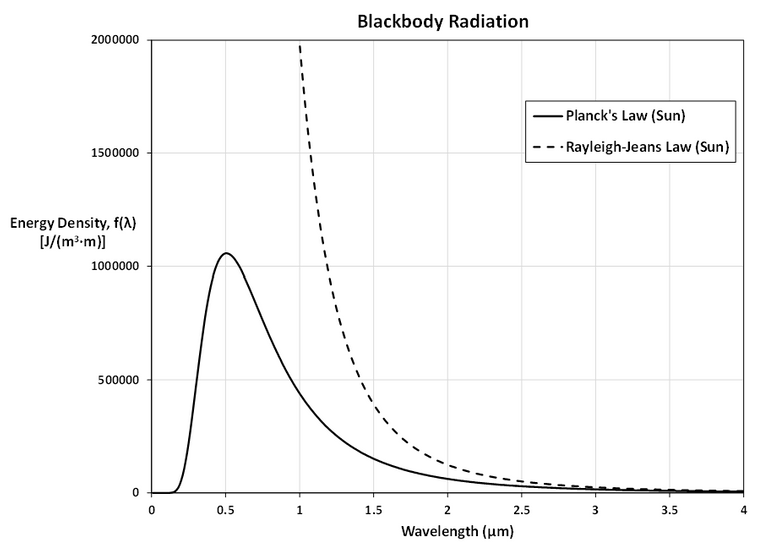
    image.png

    image.png

    The first figure shows that the two laws are similar for large λ.

    The second figure shows that the two laws are very different for short wavelengths.

    Planck's Law gives a maximum at λ ≈ 0.5 µm while the Rayleigh-Jeans Law gives no maximum or minimum.

    Solution to Question 4

    From the graph in Question 3, f(λ) has a maximum under Planck's Law at λ ≈ 0.5 µm.

    Solution to Question 5

    Using Planck's Law we can investigate how the graph of f changes for different temperatures of stars:

    • Betelgeuse: 3400 K
    • Sun: 5700 K
    • Procyon: 6400 K
    • Sirius: 9200 K

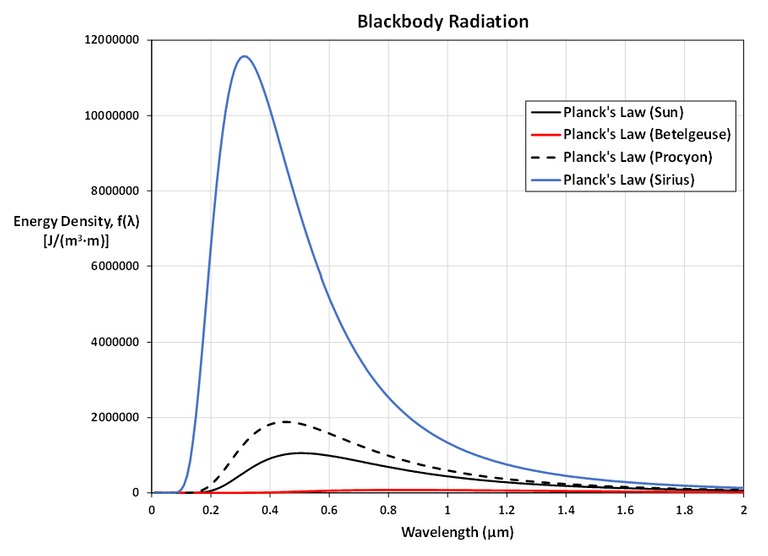
    image.png

    Here is a zoomed in look at Betelgeuse.

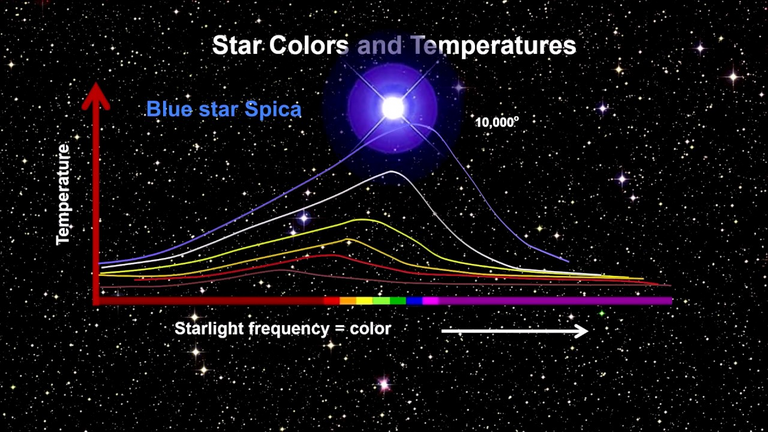
    image.png

    As T gets larger, the total area under the curve increases, as we would expect: the hotter the star, the more energy it emits.

    Also, as T increases, the λ-value of the maximum decreases (shifted to the left), so the higher the temperature, the shorter the peak wavelength (and consequently the average wavelength) of light emitted.

    This is why Sirius is a blue star and Betelgeuse is a red star: most of Sirius's light is of a fairly short wavelength; that is, a higher frequency, toward the blue end of the spectrum, whereas most of Betelgeuse's light is of a lower frequency, toward the red end of the spectrum.

    image.png

    Quick Review of Planck's Law

    For more context, let's go over a quick review of Planck's Law.

    https://en.wikipedia.org/wiki/Planck%27s_law
    Retrieved: 18 May 2021
    Archive: https://archive.ph/wip/dbFi1

    Planck's law

    Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.[1]

    At the end of the 19th century, physicists were unable to explain why the observed spectrum of black-body radiation, which by then had been accurately measured, diverged significantly at higher frequencies from that predicted by existing theories. In 1900, Max Planck heuristically [trial and error method] derived a formula for the observed spectrum by assuming that a hypothetical electrically charged oscillator in a cavity that contained black-body radiation could only change its energy in a minimal increment, E, that was proportional to the frequency of its associated electromagnetic wave. This resolved the problem of the ultraviolet catastrophe predicted by classical physics. This discovery was a pioneering insight of modern physics and is of fundamental importance to quantum theory.

    The Law

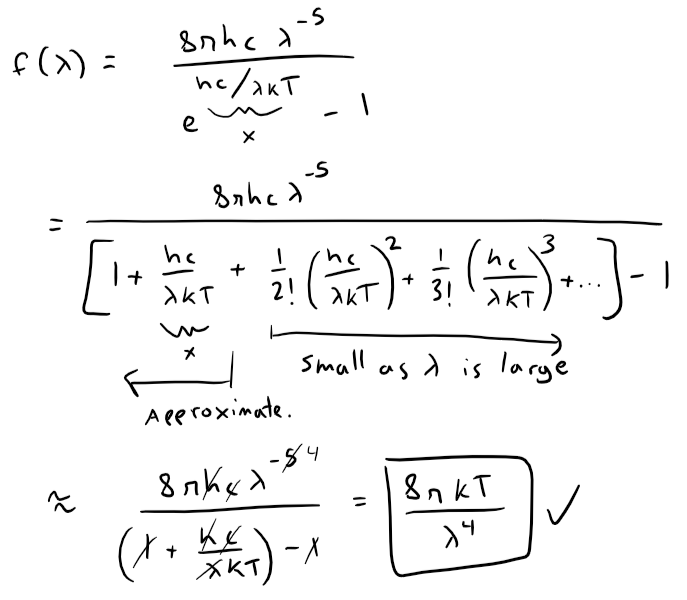
    Every physical body spontaneously and continuously emits electromagnetic radiation and the spectral radiance [wavelength/frequency spectrum of emitted radiation] of a body, B, describes the spectral emissive power per unit area, per unit solid angle [angle of projection] for particular radiation frequencies. The relationship given by Planck's radiation law, given below, shows that with increasing temperature, the total radiated energy of a body increases and the peak of the emitted spectrum shifts to shorter wavelengths.[2] According to this, the spectral radiance of a body for frequency ν at absolute temperature T is given by

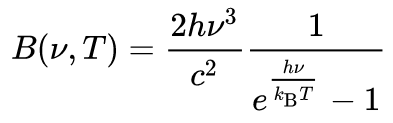
    image.png

    where kB is the Boltzmann constant, h is the Planck constant, and c is the speed of light in the medium, whether material or vacuum.[3][4][5]

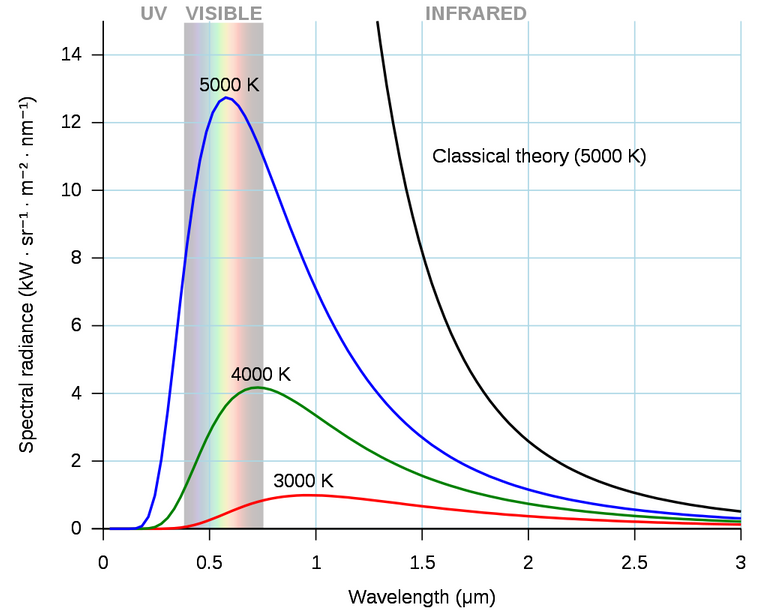
    image.png

    Planck's law accurately describes black-body radiation. Shown here are a family of curves for different temperatures. The classical (black) curve diverges from observed intensity at high frequencies (short wavelengths).

    Note that the solid angle has units of "steradians" and is the angle of the projection of a specific area on the surface of a sphere.

    image.png

    This is used to quantify the amount of radiation projected from a heat source.

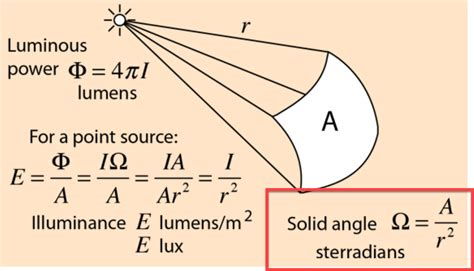
    image.png

    Note that the equation used by the above Wikipedia article is not the exact same as the one my calculus book used, but we see the version used from the following Rayleigh-Jeans Law Wiki article.

    https://en.wikipedia.org/wiki/Rayleigh%E2%80%93Jeans_law
    Retrieved: 18 May 2021
    Archive: https://archive.ph/wip/DvoIw

    Rayleigh-Jeans law

    In physics, the Rayleigh–Jeans Law is an approximation to the spectral radiance of electromagnetic radiation as a function of wavelength from a black body at a given temperature through classical arguments. For wavelength λ, it is:

    image.png

    where Bλ is the spectral radiance, the power emitted per unit emitting area, per steradian, per unit wavelength; c is the speed of light; kB is the Boltzmann constant; and T is the temperature in kelvins. For frequency v, the expression is instead

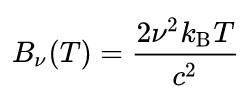
    image.png

    The Rayleigh–Jeans law agrees with experimental results at large wavelengths (low frequencies) but strongly disagrees at short wavelengths (high frequencies). This inconsistency between observations and the predictions of classical physics is commonly known as the ultraviolet catastrophe.[1][2] Its resolution in 1900 with the derivation by Max Planck of Planck's law, which gives the correct radiation at all frequencies, was a foundational aspect of the development of quantum mechanics in the early 20th century.

    …

    In other cases, Planck's law is written as

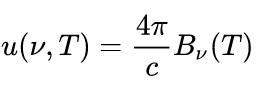
    image.png

    for energy per unit volume (energy density). In this form, the Planck function and associated Rayleigh–Jeans limits are given by

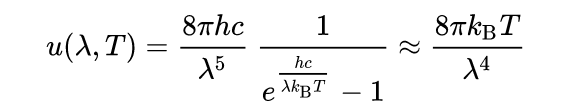
    image.png

    MES Note: These are the equations used by my calculus book in this applied project.

    or

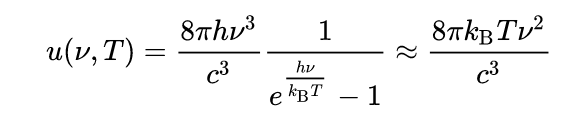
    image.png

    MES Note on Planck's Constant

    Planck's Law was able to better predict Blackbody Radiation by modeling energy as discrete packets called "quanta", which ushered in the start of Quantum Mechanics.

    I had initially written up additional information on Planck's Law and its derivation but I have since removed it as it was too far off topic from this straightforward Applied Project.

    My initial reasoning was to compare the mainstream interpretation of Planck's constant of being a "quantum of action" with Lori Gardi's interpretation that it is in fact the quantum of "energy".

    The following links I recommend as reference for further research.

    The derivation of Planck's Law involves quantizing Energy as an integer number (n) multiplied by Planck's Constant (h) multiplied by frequency (f).

    image.png

    The use of the frequency term in the quantized energy equation is interpreted as "wave-particle duality photons" with different discrete energies.

    image.png

    image.png

    The physics investigator Lori Gardi argues that since the frequency term has units of "cycles / second" then the conventional quantized energy equation is actually for a single second or unit of time.

    This means that instead of quantized energies for each frequency, light may be viewed as being made up of a single quantized energy, Planck's Constant.

    Thus, the more quantized energy units per unit time corresponds to a higher total energy.

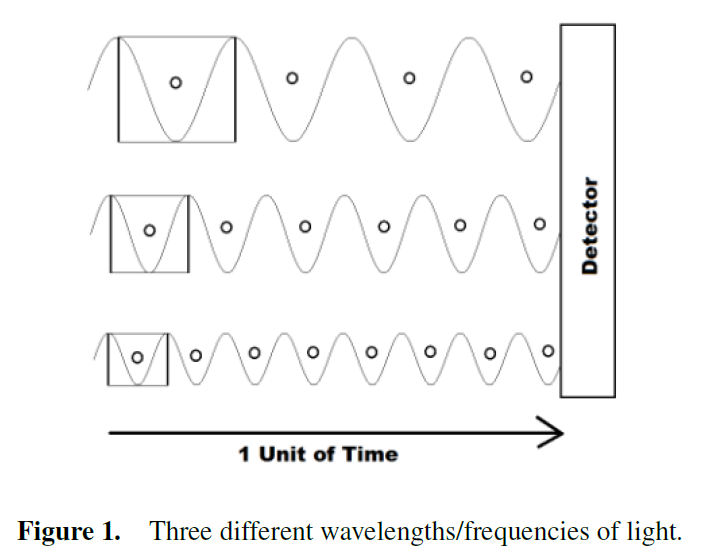
    image.png

    In this interpretation, the frequency is an emergent or more abstract concept made up many quanta of energy.

    I will be exploring this further so stay tuned!

    mathematics calculus science messcience stemgeeks education palnet physics stem quantumphysics
    0
    0
    0.000
    0 comments