¿Qué es un Ciclotrón?
En la última publicación presentada en esta plataforma, estuvimos hablando sobre J.J Thomson y su gran aporte al mundo de la ciencia con el descubrimiento del electrón, también estableció la relación e/m y para ello utilizó el principio del selector de velocidades. El día de hoy estarnos conociendo sobre El Ciclotrón.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.

Ernest Orlando Lawrence y M. Stanley Livingston en 1934 inventaron el ciclotrón. Lawrence es un químico nuclear de origen estadounidense quien principalmente se conoce por su creación y mejoramiento del ciclotrón; también es importante destacar que realizo la separación isotópica de Uranio, de igual manera fue acreedor de un premio nobel en el año 1939 por sus diversas investigaciones y fue el profesor titular más joven de la Universidad de California. Por otra parte, Livingston fue un físico acelerador estadounidense quien es co-autor de la invención de los ciclotrones, fue licenciado en Artes con una doble especialización en Química y Física; también realizó estudios sobre la difracción de rayos X.

Fuente 1 - 2
Uno de los inventos más importantes de la historia, ya que fue un gran aporte para el área de la medicina nuclear y la realización de diagnósticos mediante tomografías por la emisión de positrones. Un ciclotrón es un acelerador de partículas cargadas que puede acelerar a muy altas velocidades dichas partículas; jugando un papel muy importante las fuerzas eléctricas y magnéticas; las partículas energéticas que se producen son utilizadas para bombardear otros núcleos y con esto se producen reacciones nucleares que son d interés para diversas investigaciones.
En la imagen que se presenta a continuación podemos ver el diagrama esquemático de un ciclotrón, donde básicamente existen dos recipientes semicirculares conocidos como des (electrones en forma de D); dichos recipientes se evacuan con la finalidad de minimizar las pérdidas de energía ocasionadas por los choques entre las moléculas de aire y los iones. Entonces, un campo magnético uniforme que se genera por un electroimán que se mueve hacia la des, al cual se le aplica un voltaje alterno de alta frecuencia.
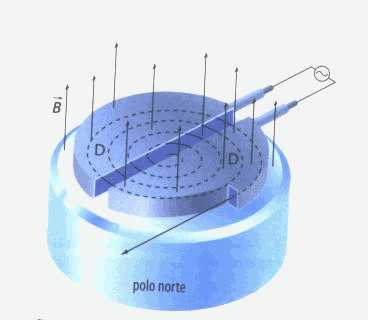
Fuente
Ahora bien, los iones positivos liberados cerca del centro del imán, los cuales se mueven en trayectoria semicircular y luego regresan al entrehierro un tiempo de T/2, sabiendo que T es el periodo de revolución, el cual se expresa de la siguiente manera:
Con respecto a la frecuencia del voltaje que se aplica, también se ajusta de manera tal que la polaridad del des se invierte en el mismo tiempo que es igual al que tardan los iones en completar la mitad de una revolución. Ahora, si la fase del voltaje que se aplica se ajusta de tal manera que el recipiente 2 se encuentra a un potencial menor que el recipiente 1, mientras que su energía cinética se incrementa en una radio aún más grande. Al cabo de un tiempo igual a T/2, vuelve a llegar al entrehierro, justo en ese momento se produce la inversión del potencial mediante de la des, por lo que ahora el recipiente 1 es negativo y al ion se le da otro empujón a través del entrehierro. Al mismo tiempo, el movimiento continua de tal manera que cada media revolución el ion va ganando energía cinética que es igual a qV, a medida que el radio de su órbita es prácticamente el de la des y finalmente el ion energético deja el sistema mediante la rejilla de salida.
Un aspecto muy importante de resaltar es que la operación del ciclotrón se centra en el hecho de que el tiempo que tarda una revolución es independiente de la velocidad del ion o del radio de su órbita. Para un ciclotrón, existe una expresión para la energía cinética del ion cuando él sale del ciclotrón y está en función del radio, la misma se plantea de la siguiente manera:
Finalmente es importante acotar que cuando la energía de los iones es mayor que 20MeV, se presentan efectos relativistas y la masa del ion deja de ser constante. Es por ello, que el periodo de la órbita va en aumento y los iones en rotación no están en fase con el voltaje aplicado.

En este momento, resulta propicio poder ver desde el punto de vista práctico cómo se comporta un ciclotrón. Si se diseña un ciclotrón para acelerar protones tiene un campo magnético de 0,45 T de magnitud sobre una región de 1,2 m de radio. ¿Cuáles son la frecuencia del ciclotrón y la velocidad máxima que adquieren los protones?
Este es un ejemplo muy sencillo de resolver, se trata de un acelerador de protones específicamente con un campo magnético y un radio, del cual nos piden determinar la frecuencia del ciclotrón y la velocidad máxima. Veamos cuales son los datos:
Entre las incógnitas están:
Entonces procedemos a calcular la frecuencia del ciclotrón, sabiendo que.
Ahora vamos a despejar v.
Pero nosotros sabemos que según el movimiento circular.
Entonces podemos sustituir y decir que:
Si introducimos los valores dentro de la ecuación, tenemos que:
Para completar el enunciado y calcular la velocidad máxima del protón, partimos de la ecuación de la velocidad lineal del movimiento circular.
Sustituimos
En conclusión, podemos destacar que la frecuencia del ciclotrón es de 0,43 x 10 exp 8 radianes sobre segundo, y la velocidad máxima que adquieren los protones es de 0,517 x 10 exp 8 metros sobre segundo.

Referencias
Hewitt, P. (2007). Física Conceptual. México: Pearson Educación.
Serway, R &. (1997). Física Tomo II. México: McGrawHill.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.



0
0
0.000
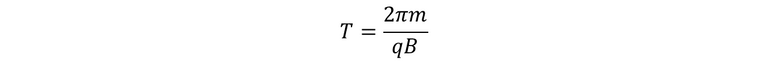
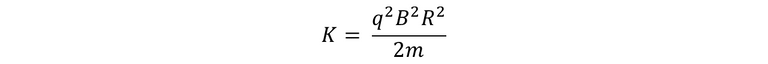


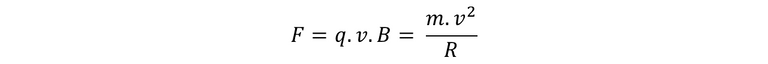
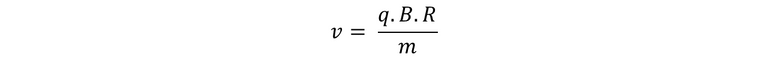
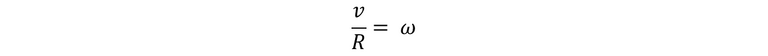
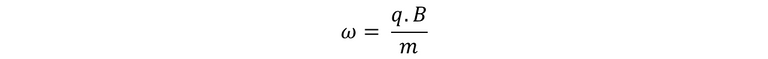
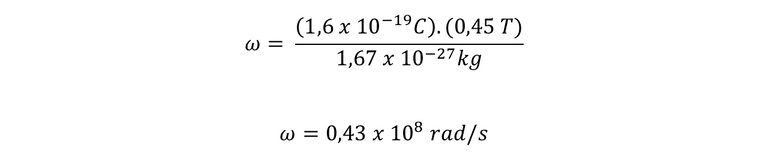
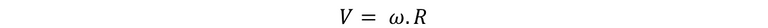
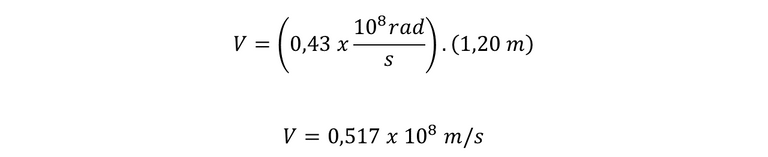
https://twitter.com/345684731/status/1592288706932662274
The rewards earned on this comment will go directly to the people sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
https://twitter.com/ILovePhysica/status/1592288706932662274?s=20&t=PYZpVFsiXNMa9VR3jUMUyA
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Su post ha sido valorado por @ramonycajal